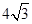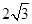题目内容
在斜三角形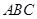 中,角A,B,C的对边分别为 a,b,c.
中,角A,B,C的对边分别为 a,b,c.
(1)若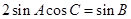 ,求
,求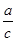 的值;
的值;
(2)若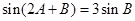 ,求
,求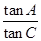 的值.
的值.
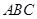 中,角A,B,C的对边分别为 a,b,c.
中,角A,B,C的对边分别为 a,b,c.(1)若
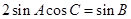 ,求
,求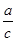 的值;
的值;(2)若
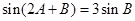 ,求
,求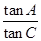 的值.
的值.(1)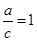 ,(2)
,(2)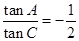 .
.
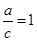 ,(2)
,(2)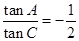 .
.试题分析:(1)解三角形问题,一般利用正余弦定理进行变角转化. 因为
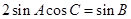 ,所以由正余弦定理,得
,所以由正余弦定理,得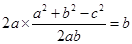 ,整理得
,整理得 ,即
,即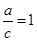 .本题也可化角:
.本题也可化角: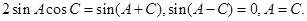 (2)在斜三角形
(2)在斜三角形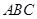 中,
中,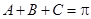 ,所以
,所以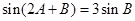 可化为
可化为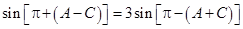 ,即
,即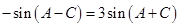 .故
.故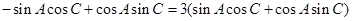 .整理,得
.整理,得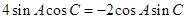 ,因为△ABC是斜三角形,所以sinAcosAcosC
,因为△ABC是斜三角形,所以sinAcosAcosC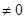 ,所以
,所以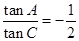 .
.解:(1)由正弦定理,得
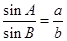 .
.从而
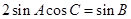 可化为
可化为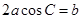 . 3分
. 3分由余弦定理,得
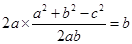 .
.整理得
 ,即
,即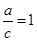 . 7分
. 7分(2)在斜三角形
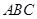 中,
中,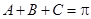 ,
,所以
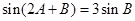 可化为
可化为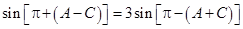 ,
,即
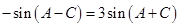 . 10分
. 10分故
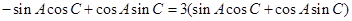 .
.整理,得
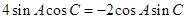 , 12分
, 12分因为△ABC是斜三角形,所以sinAcosAcosC
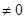 ,
,所以
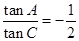 . 14分
. 14分
练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
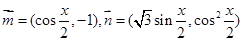 ,设函数
,设函数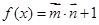 .
.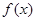 的单调递增区间;
的单调递增区间;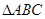 中,角
中,角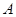 、
、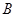 、
、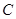 的对边分别为
的对边分别为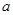 、
、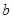 、
、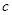 ,且满足
,且满足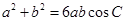 ,
,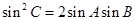 ,求
,求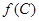 的值.
的值.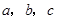 ,已知
,已知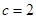 ,
,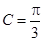 .
.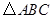 的面积等于
的面积等于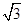 ,求
,求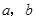 ;
;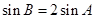 ,求
,求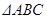 的内角
的内角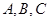 的对边分别为
的对边分别为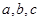 ,且
,且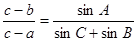 , 则
, 则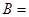 ______
______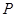 .
.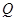 的大小; (2)求△ABC面积的最大值.
的大小; (2)求△ABC面积的最大值.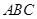 中,角
中,角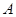 ,
,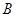 ,
,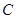 的对边分别是
的对边分别是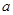 ,
,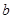 ,
,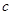 ,且
,且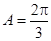 ,
,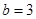 ,△
,△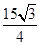 .
.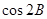 的值.
的值.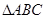 中,
中,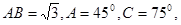 则BC =( )
则BC =( )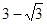
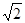
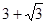
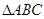 中,边
中,边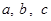 所对角分别为
所对角分别为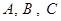 ,若
,若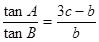 ,
,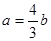 ,则
,则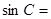 ( )
( )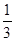
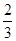
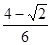
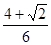
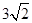 ,则AC=
,则AC=