题目内容
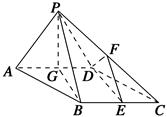
如图,在四棱锥P-ABCD中,底面ABCD是∠DAB=60°,且边长为a的菱形,侧面PAD为正三角形,其所在平面垂直底面ABCD.

(1)若G为AD边的中点,求证:BG⊥平面PAD;
(2)求证:AD⊥PB;
(3)若E为BC边的中点,能否在棱PC上找到一点F,使平面DEF⊥平面ABCD,并证明你的结论.

(1)若G为AD边的中点,求证:BG⊥平面PAD;
(2)求证:AD⊥PB;
(3)若E为BC边的中点,能否在棱PC上找到一点F,使平面DEF⊥平面ABCD,并证明你的结论.
(1)见解析 (2)见解析
(3)当F为PC的中点时,满足平面DEF⊥平面ABCD.见解析
(3)当F为PC的中点时,满足平面DEF⊥平面ABCD.见解析
(1)证明:∵在菱形ABCD中,∠DAB=60°,
G为AD的中点,得BG⊥AD.
又平面PAD⊥平面ABCD,
平面PAD∩平面ABCD=AD,∴BG⊥平面PAD.
(2)证明:连结PG,因为△PAD为正三角形,G为AD的中点,得PG⊥AD.
由(1)知BG⊥AD,
∵PG∩BG=G,PG?平面PGB,BG?平面PGB
∴AD⊥平面PGB.
∵PB?平面PGB,∴AD⊥PB.
(3)解:当F为PC的中点时,满足平面DEF⊥平面ABCD.
证明如下:取PC的中点F,连结DE,EF,DF,则在△PBC中,FE∥PB,在菱形ABCD中,GB∥DE,而FE?平面DEF,DE?平面DEF,FE∩DE=E,∴平面DEF∥平面PGB.
由(2)可知,PG⊥平面ABCD,而PG?平面PGB,∴平面PGB⊥平面ABCD,∴平面DEF⊥平面ABCD.
G为AD的中点,得BG⊥AD.

又平面PAD⊥平面ABCD,
平面PAD∩平面ABCD=AD,∴BG⊥平面PAD.
(2)证明:连结PG,因为△PAD为正三角形,G为AD的中点,得PG⊥AD.
由(1)知BG⊥AD,
∵PG∩BG=G,PG?平面PGB,BG?平面PGB
∴AD⊥平面PGB.
∵PB?平面PGB,∴AD⊥PB.
(3)解:当F为PC的中点时,满足平面DEF⊥平面ABCD.
证明如下:取PC的中点F,连结DE,EF,DF,则在△PBC中,FE∥PB,在菱形ABCD中,GB∥DE,而FE?平面DEF,DE?平面DEF,FE∩DE=E,∴平面DEF∥平面PGB.
由(2)可知,PG⊥平面ABCD,而PG?平面PGB,∴平面PGB⊥平面ABCD,∴平面DEF⊥平面ABCD.

练习册系列答案
相关题目
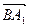 ,
, )的值;
)的值;
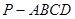 中,底面
中,底面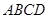 为矩形,
为矩形,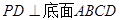 ,
,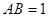 ,
,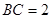 ,
,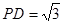 ,
, 分别为
分别为 的中点.
的中点.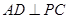 ;
; 平面
平面 ;
;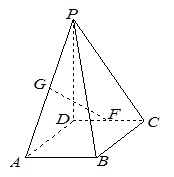
 ,BC=,求二面角S-AB-C的余弦值.
,BC=,求二面角S-AB-C的余弦值.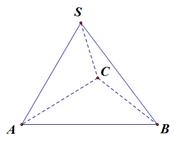

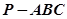 中,
中, ,
,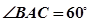 ,
,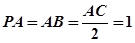 ,
,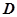 ,
,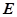 分别是
分别是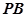 ,
,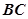 中点.
中点.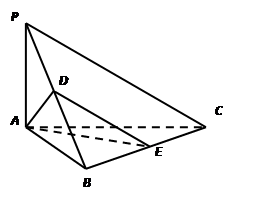
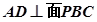 ;
;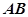 与平面
与平面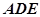 所成角的正弦值.
所成角的正弦值.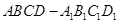 中,底面
中,底面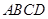 是等腰梯形,
是等腰梯形,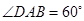 ,
,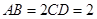 ,
,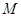 是线段
是线段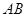 的中点.
的中点.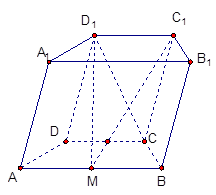
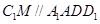 ;
;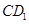 垂直于平面
垂直于平面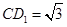 ,求平面
,求平面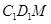 和平面
和平面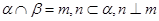 ,则
,则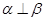 ;②若
;②若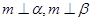 ,则
,则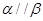 ;③若
;③若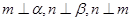 ,则
,则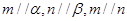 ,则
,则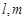 与平面
与平面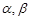 的命题中,正确的是( )
的命题中,正确的是( ) 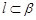 且
且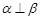 ,则
,则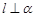
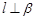 且
且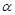 ∥
∥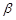 ,则
,则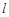 ∥
∥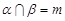 ,且
,且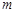 ,则
,则