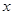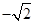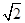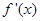题目内容
设函数 ,
,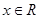
(Ⅰ)求函数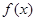 的单调区间;
的单调区间;
(Ⅱ)求函数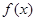 在区间
在区间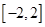 上的最值.
上的最值.
【答案】
(Ⅰ) 的单调递增区间为
的单调递增区间为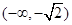 和
和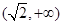 , 单调递减区间为
, 单调递减区间为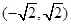 ;(Ⅱ)函数
;(Ⅱ)函数 在区间
在区间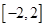 上的最大值为
上的最大值为 ,最小值为
,最小值为 .
.
【解析】
试题分析:(Ⅰ)求函数 的单调区间,它的解题方法有两种:一是利用定义,二是导数法,本题由于是三次函数,可用导数法求单调区间,只需求出
的单调区间,它的解题方法有两种:一是利用定义,二是导数法,本题由于是三次函数,可用导数法求单调区间,只需求出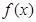 的导函数,判断
的导函数,判断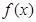 的导函数的符号,从而求出
的导函数的符号,从而求出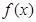 的单调区间;(Ⅱ)求函数
的单调区间;(Ⅱ)求函数 在区间
在区间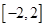 上的最值,求
上的最值,求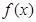 在区间
在区间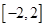 上的最大值,此题属于函数在闭区间上的最值问题,解此类题,只需求出极值,与端点处的函数值,比较谁大,就取谁,本题比较简单,属于送分题.
上的最大值,此题属于函数在闭区间上的最值问题,解此类题,只需求出极值,与端点处的函数值,比较谁大,就取谁,本题比较简单,属于送分题.
试题解析:(Ⅰ)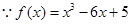 ,
, 令
令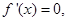
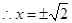
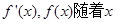 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
0 |
— |
0 |
|
|
|
单调递增 |
极大值 |
单调递减 |
极小值 |
单调递增 |
由上表可知 的单调递增区间为
的单调递增区间为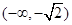 和
和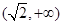 , 单调递减区间为
, 单调递减区间为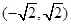 .
.
(Ⅱ)由(Ⅰ)可知函数 在
在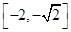 上单调递增,在
上单调递增,在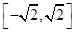 上单调递减,在
上单调递减,在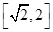 上单调递增,
上单调递增, 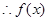 的极大值
的极大值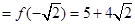 ,
,  的极小值
的极小值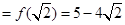
又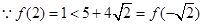 ,
, 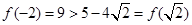
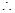 函数
函数 在区间
在区间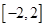 上的最大值为
上的最大值为 ,最小值为
,最小值为 .
.
考点:本题函数与导数,导数与函数的单调性、导数与函数的极值及最值,学生的基本推理能力,学生的基本运算能力以及转化与化归的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目