题目内容
已知函f(x)=ln x,g(x)=| 1 | 2 |
(1)若a=-2时,函h(x)=f(x)-g(x),在其定义域是增函数,求b的取值范围;
(2)在(1)的结论下,设函数φ(x)=e2x+bex,x∈[0,ln2],求函数φ(x)的最小值;
(3)当a=-2,b=4时,求证2x-f(x)≥g(x)-3.
分析:(1)、将a=-2代入h(x)=f(x)-g(x)中,求得h(x)的解析式,然后求出其导数,利用导数的性质结合题中已知条件便可求出b的取值范围;
(2)根据题意先求出φ(x)的解析式,然后分别讨论当-
≤1,1<-
<2和-
≥2时函数φ(x)的最小值;
(3)将a=-2,b=4代入其中,令h(x)=2lnx+x+
,求出函数h(x)的最小值,便可证明2x-f(x)≥g(x)-3.
(2)根据题意先求出φ(x)的解析式,然后分别讨论当-
| b |
| 2 |
| b |
| 2 |
| b |
| 2 |
(3)将a=-2,b=4代入其中,令h(x)=2lnx+x+
| 3 |
| x |
解答:解:(1)依题意:h(x)=ln x+x2-bx,h(x)在(0,+∞)上是增函数,
∴h′(x)=
+2x-b≥0对x∈(0,+∞)恒成立,
∴b≤
+2∵x>0,则
+2x≥2(当x═
时取等号).
∴b的取值范围为(-∞,2
].
(2)设t=ex,则函数化为y=t2+bt,t∈[1,2],∵y=(t+
)2-
,
∴①当-
≤1,即-2≤b≤2
时,函数y在[1,2]上为增函数,
当t=1时,ymin=b+1.
②当1<-
<2,即-4<b<-2时,当t=-
时,ymin=-
.
③当-
≥2,即b≤4时,函数y在[1,2]上为减函数,当t=2时,ymin=-4+2b.
综上所述,当-2≤-
≤2
时,φ(x)min=b+1;
当-4<b<-2时,φ(x)min=-
;
当b≤4时,φ(x)min=4+2b.
(3)要证2xlnx≥-x2+4x-3,只要证4≤2lnx+x+
,
设h(x)=2lnx+x+
(x>0),则h′(x)=
,
x∈(0,1),h′(x)<0,∴h(x)单调递减;
x∈(1,+∞),h′(x)>0,h(x)单调递增,
∴h(x)min=h(1)=4,
∴对一切x∈(0,+∞),2x-f(x)≥g(x)-3恒成立.
∴h′(x)=
| 1 |
| x |
∴b≤
| 1 |
| x |
| 1 |
| x |
| ||
| 2 |
∴b的取值范围为(-∞,2
| 2 |
(2)设t=ex,则函数化为y=t2+bt,t∈[1,2],∵y=(t+
| b |
| 2 |
| b2 |
| 4 |
∴①当-
| b |
| 2 |
| 2 |
当t=1时,ymin=b+1.
②当1<-
| b |
| 2 |
| b |
| 2 |
| b2 |
| 4 |
③当-
| b |
| 2 |
综上所述,当-2≤-
| b |
| 2 |
| 2 |
当-4<b<-2时,φ(x)min=-
| b2 |
| 2 |
当b≤4时,φ(x)min=4+2b.
(3)要证2xlnx≥-x2+4x-3,只要证4≤2lnx+x+
| 3 |
| x |
设h(x)=2lnx+x+
| 3 |
| x |
| (x+3)(x-1) |
| x2 |
x∈(0,1),h′(x)<0,∴h(x)单调递减;
x∈(1,+∞),h′(x)>0,h(x)单调递增,
∴h(x)min=h(1)=4,
∴对一切x∈(0,+∞),2x-f(x)≥g(x)-3恒成立.
点评:本题主要考查了利用导数求闭区间上函数的最值和函数的单调性,考查了学生的计算能力和对函数的综合掌握,解题时注意分类讨论的数学思想的运用,是各地高考的常考题,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ax2+bx(a≠0).
ax2+bx(a≠0). ax2+bx(a≠0).
ax2+bx(a≠0).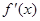 为f(x)的导函数,求证:
为f(x)的导函数,求证:
