题目内容
 如图:已知正方体ABCD-A1B1C1D1,过BD1的平面分别交棱AA1和棱CC1于E、F两点.
如图:已知正方体ABCD-A1B1C1D1,过BD1的平面分别交棱AA1和棱CC1于E、F两点.(1)求证:A1E=CF;
(2)若E、F分别是棱AA1和棱CC1的中点,求证:平面EBFD1⊥平面BB1D1.
分析:(1)由正方体的结构特征,结合已知中过BD1的平面分别交棱AA1和棱CC1于E、F两点,根据面面平行的性质定理,可得D1E∥BF,BE∥D1F,即四边形EBFD1为平行四边形,进而由HL可证得Rt△A1D1E≌Rt△CB,由全等三角形的性质可得A1E=CF;
(2)若E、F分别是棱AA1和棱CC1的中点,易得四边形EBFD1为菱形.连接EF、BD1、A1C1.则四边形EBFD1为菱形,由正方形的结构特征及菱形的性质,可证得EF⊥平面BB1D1,进而根据面面垂直的判定定理可得平面EBFD1⊥平面BB1D1.
(2)若E、F分别是棱AA1和棱CC1的中点,易得四边形EBFD1为菱形.连接EF、BD1、A1C1.则四边形EBFD1为菱形,由正方形的结构特征及菱形的性质,可证得EF⊥平面BB1D1,进而根据面面垂直的判定定理可得平面EBFD1⊥平面BB1D1.
解答:解:(1)证明:由题知,平面EBFD1与平面BCC1B1交于BF、与平面ADD1A交于ED1 …(1分)
又平面BCC1B1∥平面ADD1A1
∴D1E∥BF …(2分)
同理BE∥D1F …(3分)
∴四边形EBFD1为平行四边形
∴D1E=BF …(4分)
∵A1D1═CB,D1E=BF,∠D1A1E=∠BCF=90°
∴Rt△A1D1E≌Rt△CBF
∴A1E=CF …(6分)
(2)∵四边形EBFD1是平行四边形.AE=A1E,FC=FC1,
∴Rt△EAB≌Rt△FCB,
∴BE=BF,故四边形EBFD1为菱形. …(8分)
连接EF、BD1、A1C1.∵四边形EBFD1为菱形,∴EF⊥BD1,
在正方体ABCD-A1B1C1D1中,有B1D1⊥A1C1,B1D⊥A1A
∴B1D1⊥平面A1ACC1. …(10分)
又EF?平面A1ACC1,∴EF⊥B1D1.又B1D1∩BD1=D1,
∴EF⊥平面BB1D1.
又EF?平面EBFD1,故平面EBFD1⊥平面BB1D1. …(12分)
又平面BCC1B1∥平面ADD1A1
∴D1E∥BF …(2分)
同理BE∥D1F …(3分)
∴四边形EBFD1为平行四边形
∴D1E=BF …(4分)
∵A1D1═CB,D1E=BF,∠D1A1E=∠BCF=90°
∴Rt△A1D1E≌Rt△CBF
∴A1E=CF …(6分)
(2)∵四边形EBFD1是平行四边形.AE=A1E,FC=FC1,
∴Rt△EAB≌Rt△FCB,
∴BE=BF,故四边形EBFD1为菱形. …(8分)
连接EF、BD1、A1C1.∵四边形EBFD1为菱形,∴EF⊥BD1,
在正方体ABCD-A1B1C1D1中,有B1D1⊥A1C1,B1D⊥A1A
∴B1D1⊥平面A1ACC1. …(10分)
又EF?平面A1ACC1,∴EF⊥B1D1.又B1D1∩BD1=D1,
∴EF⊥平面BB1D1.
又EF?平面EBFD1,故平面EBFD1⊥平面BB1D1. …(12分)
点评:本题考查的知识点是平面与平面垂直的判定,平面与平面平行的性质,其中(1)的关键是由面面平行的性质定义证得D1E∥BF,BE∥D1F,进而得到四边形EBFD1为平行四边形,(2)的关键是证得EF⊥平面BB1D1.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
 8、如图,已知正方体ABCD-A1B1C1D1的棱长为3,点E,F在线段AB上,点M在线段B1C1上,点N在线段C1D1上,且EF=1,D1N=x,AE=y,M是B1C1的中点,则四面体MNEF的体积( )
8、如图,已知正方体ABCD-A1B1C1D1的棱长为3,点E,F在线段AB上,点M在线段B1C1上,点N在线段C1D1上,且EF=1,D1N=x,AE=y,M是B1C1的中点,则四面体MNEF的体积( )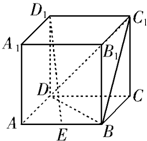 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E为棱AB的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E为棱AB的中点. 如图,已知正方体ABCD-A1B1C1D1的棱长为2,E、F分别是D1C、AB的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,E、F分别是D1C、AB的中点. 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P,Q,R分别是棱AB,CC1,D1A1的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P,Q,R分别是棱AB,CC1,D1A1的中点. (2012•宝山区一模)如图,已知正方体ABCD-A1B1C1D1 的棱长为2,E,F分别是BB1,CD的中点.
(2012•宝山区一模)如图,已知正方体ABCD-A1B1C1D1 的棱长为2,E,F分别是BB1,CD的中点.