题目内容
(本小题满分14分)
求函数 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.
求函数
 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.函数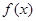 在
在 上的最小值为
上的最小值为 ,最大值为
,最大值为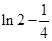
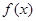 在
在 上的最小值为
上的最小值为 ,最大值为
,最大值为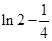
∵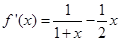 ,令
,令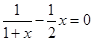 ,即
,即 ,
,
解得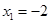 (舍去),
(舍去),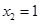 .
.
当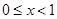 时,
时,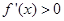 ,
,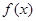 单调递增;当
单调递增;当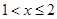 时,
时,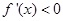 ,
,
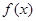 单调递减.∴
单调递减.∴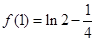 为函数
为函数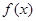 的极大值.
的极大值.
又∵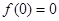 ,
,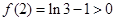 ,
,
∴函数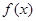 在
在 上的最小值为
上的最小值为 ,最大值为
,最大值为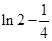
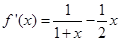 ,令
,令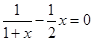 ,即
,即 ,
,解得
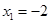 (舍去),
(舍去),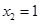 .
.当
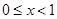 时,
时,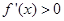 ,
,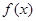 单调递增;当
单调递增;当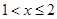 时,
时,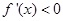 ,
, 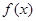 单调递减.∴
单调递减.∴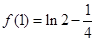 为函数
为函数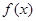 的极大值.
的极大值.又∵
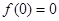 ,
,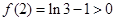 ,
,∴函数
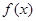 在
在 上的最小值为
上的最小值为 ,最大值为
,最大值为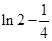

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,其长为32米,宽为18米,现要在此空地上种植一块矩形草坪,三边留有人行道,人行道宽度为
,其长为32米,宽为18米,现要在此空地上种植一块矩形草坪,三边留有人行道,人行道宽度为 米与
米与 米均不小于2米,且要求“转角处”(图中矩形
米均不小于2米,且要求“转角处”(图中矩形 )的面积为8平方米
)的面积为8平方米 ,并指出
,并指出
 的图象是
的图象是
 ,
, ,且
,且 ;
; ;
; 时,
时,
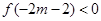 恒成立,求实数
恒成立,求实数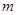 的取值范围。
的取值范围。 (
( R,a为常数);②
R,a为常数);② ;③当
;③当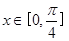 时,
时, ≤2。
≤2。 的解析式;(Ⅱ)常数a的取值范围。
的解析式;(Ⅱ)常数a的取值范围。 城周边已有两条公路
城周边已有两条公路 在点O处交汇,且它们的夹角为
在点O处交汇,且它们的夹角为 .已知
.已知 ,
,  与公路
与公路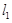 夹角为
夹角为 .现规划在公路
.现规划在公路 两处作为交汇点(异于点O)直接修建一条公路通过
两处作为交汇点(异于点O)直接修建一条公路通过
 ,
,
 关于
关于 的函数关系式并指出它的定义域;
的函数关系式并指出它的定义域; 的面积最小.
的面积最小.
 满足
满足 ="1" 且
="1" 且 ,则
,则 =___________。
=___________。 ,那么
,那么
 ( )
( ) 


