题目内容
在△ABC中,∠C=90°, =(k,1),
=(k,1), 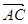 =(2,3),则k的值是( )
=(2,3),则k的值是( )
| A.5 | B.-5 | C. | D.- 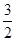 |
A
解析试题分析: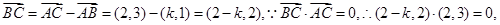
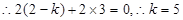
考点:考查了向量的坐标运算,以及向量垂直的坐标表示.
点评:解本小题关键是根据向量的运算法则求出向量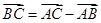 的坐标,再根据
的坐标,再根据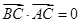 建立关于k的方程求出k值.
建立关于k的方程求出k值.

练习册系列答案
相关题目
已知向量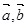 满足
满足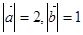 ,其夹角为
,其夹角为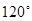 ,若对任意向量
,若对任意向量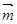 ,总有
,总有 ,则
,则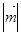 的最大值与最小值之差为
的最大值与最小值之差为
| A.1 | B.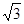 | C.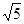 | D.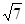 |
向量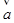 = (cosθ, sinθ),
= (cosθ, sinθ),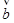 = (
= (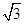 , 1),则
, 1),则 的最大值为( )
的最大值为( )
| A.3 | B.4 | C.5 | D.6 |
设向量a,b均为单位向量,且|a+b|=1,则向量a与b的夹角为( )
A.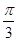 | B.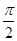 | C.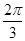 | D.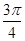 |
若向量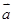 =(1,1),
=(1,1),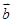 =(2,5),
=(2,5),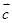 =(3,
=(3, )满足条件(8
)满足条件(8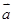 —
—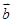 )·
)·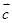 =30,则
=30,则 =
=
| A.6 | B.5 | C.4 | D.3 |
已知平面向量 ,
,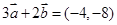 ,则
,则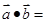 ( )
( )
| A.-10 | B.10 | C.-20 | D.20 |
已知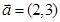 ,
,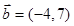 ,则向量
,则向量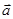 在
在 方向上设射影的数量为( )
方向上设射影的数量为( )
A.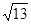 | B.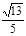 | C.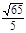 | D.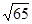 |
设向量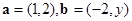 ,若
,若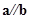 ,则
,则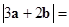
A.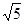 | B.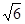 | C.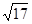 | D.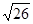 |
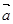 =(-3,2),
=(-3,2),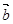 =(-1,0),向量
=(-1,0),向量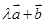 与
与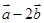 垂直,则实数
垂直,则实数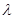 的值为 .
的值为 .