题目内容
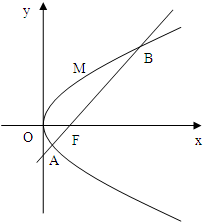 如图,斜率为1的直线过抛物线y2=2px(p>0)的焦点,与抛物线交于两点A、B,M为抛物线弧AB上的动点.
如图,斜率为1的直线过抛物线y2=2px(p>0)的焦点,与抛物线交于两点A、B,M为抛物线弧AB上的动点.(1)若|AB|=8,求抛物线的方程;
(2)求S△ABM的最大值.
分析:(1)先联立直线方程和抛物线方程,得到x1+x2的值,再根据抛物线定义,得到焦点弦的弦长公式,
代入并解得p,从而求得抛物线的方程为y2=4x.
(2)设M(
,y0),根据直线AB的方程得到用y0和p表示的点M到AB的距离d.又根据点M在直线AB的上方
解得y0的范围,即求出了d的最大值,再代入面积公式,可求得S△ABM的最大值.
代入并解得p,从而求得抛物线的方程为y2=4x.
(2)设M(
| ||
| 2p |
解得y0的范围,即求出了d的最大值,再代入面积公式,可求得S△ABM的最大值.
解答:解:(1)由条件知lAB:y=x-
,则
,
消去y得:x2-3px+
p2=0,
则x1+x2=3p,由抛物线定义得|AB|=x1+x2+p=4p
又因为|AB|=8,即p=2,则抛物线的方程为y2=4x.
(2)由(1)知|AB|=4p和lAB:y=x-
,设M(
,y0),
则M到AB的距离为:d=
,
因点M在直线AB的上方,所以-
+y0+
>0
则d=
(-
+y0+
)=
[-
(y0-p)2+p]
由x2-3px+
p2=0知A(
p,(1-
)p),B(
p,(1+
)p)
所以(1-
)p<y0<(1+
)p,则当y0=p时,dmax=
p
则(S△ABM)max=
•4p•
p=
p2
| p |
| 2 |
|
消去y得:x2-3px+
| 1 |
| 4 |
则x1+x2=3p,由抛物线定义得|AB|=x1+x2+p=4p
又因为|AB|=8,即p=2,则抛物线的方程为y2=4x.
(2)由(1)知|AB|=4p和lAB:y=x-
| p |
| 2 |
| ||
| 2p |
则M到AB的距离为:d=
|-
| ||||||
|
因点M在直线AB的上方,所以-
| 1 |
| 2p |
| y | 2 0 |
| P |
| 2 |
则d=
| ||
| 2 |
| 1 |
| 2p |
| y | 2 0 |
| p |
| 2 |
| ||
| 2 |
| 1 |
| 2p |
由x2-3px+
| 1 |
| 4 |
3-2
| ||
| 2 |
| 2 |
3+2
| ||
| 2 |
| 2 |
所以(1-
| 2 |
| 2 |
| ||
| 2 |
则(S△ABM)max=
| 1 |
| 2 |
| ||
| 2 |
| 2 |
点评:本题考查抛物线的定义,及焦点弦公式,关键是点到直线的距离公式的灵活运用和抛物线上点坐标的巧妙设法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,斜率为1的直线过抛物线Ω:y2=2px(p>0)的焦点F,与抛物线交于两点A,B,
如图,斜率为1的直线过抛物线Ω:y2=2px(p>0)的焦点F,与抛物线交于两点A,B, 如图,斜率为1的直线过抛物线y2=2px(p>0)的焦点,与抛物线交于两点A、B,将直线AB按向量
如图,斜率为1的直线过抛物线y2=2px(p>0)的焦点,与抛物线交于两点A、B,将直线AB按向量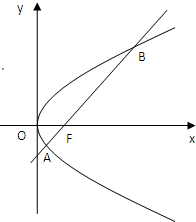 如图,斜率为1的直线过抛物线y2=2px(p>0)的焦点,与抛物线交于两点A、B,将直线AB按向量
如图,斜率为1的直线过抛物线y2=2px(p>0)的焦点,与抛物线交于两点A、B,将直线AB按向量 过抛物线
过抛物线 的焦点F,与抛物线交于两点A,B。
的焦点F,与抛物线交于两点A,B。 的方程;
的方程; 的面积S的最大值;
的面积S的最大值;