题目内容
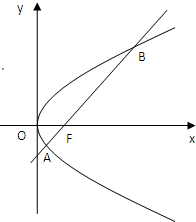 如图,斜率为1的直线过抛物线y2=2px(p>0)的焦点,与抛物线交于两点A、B,将直线AB按向量
如图,斜率为1的直线过抛物线y2=2px(p>0)的焦点,与抛物线交于两点A、B,将直线AB按向量| a |
(1)若|AB|=8,求抛物线的方程;
(2)求
| NA |
| NB |
分析:(1)根据抛物线的定义得到|AB|=x1+x2+p=4p,再由已知条件,得到抛物线的方程;
(2)设直线l的方程及N点坐标和A(x1,y1),B(x2,y2),利用向量坐标运算,求得
•
的以N点坐标表示的函数式,利用二次函数求最值的方法,可求得所求的最小值.
(2)设直线l的方程及N点坐标和A(x1,y1),B(x2,y2),利用向量坐标运算,求得
| NA |
| NB |
的以N点坐标表示的函数式,利用二次函数求最值的方法,可求得所求的最小值.
解答:解:(1)由条件知lAB:y=x-
,则
,消
去y得:x2-3px+
p2=0,则x1+x2=3p,
由抛物线定义得|AB|=x1+x2+p=4p
又因为|AB|=8,即p=2,则抛物线的方程为y2=4x.
(2)直线l的方程为:y=x+
,于是设N(x0,x0+
),A(x1,y1),B(x2,y2)
则
=(x1-x0,y1-x0-
),
=(x2,y2-x0-
)
即
•
=x1x2-x0(x1+x2)+
+y1y2-(x0+
)(y1+y2)+(x0+
)2
由第(1)问的解答结合直线方程,不难得出x1+x2=3p,x1x2=
p2
且y1+y2=x1+x2-p=2p,y1y2=(x1-
)(x2-
)=-p2
则
•
=2
-4px0-
p2=2(x0-p)2-
p2
当x0=
时,
•
的最小值为-
p2
| p |
| 2 |
|
去y得:x2-3px+
| 1 |
| 4 |
由抛物线定义得|AB|=x1+x2+p=4p
又因为|AB|=8,即p=2,则抛物线的方程为y2=4x.
(2)直线l的方程为:y=x+
| p |
| 2 |
| p |
| 2 |
则
| NA |
| p |
| 2 |
| NB |
| P |
| 2 |
即
| NA |
| NB |
| x | 2 0 |
| p |
| 2 |
| p |
| 2 |
由第(1)问的解答结合直线方程,不难得出x1+x2=3p,x1x2=
| 1 |
| 4 |
且y1+y2=x1+x2-p=2p,y1y2=(x1-
| p |
| 2 |
| p |
| 2 |
则
| NA |
| NB |
| x | 2 0 |
| 3 |
| 2 |
| 7 |
| 2 |
当x0=
| p |
| 2 |
| NA |
| NB |
| 7 |
| 2 |
点评:此题考查抛物线的定义,及向量坐标运算.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
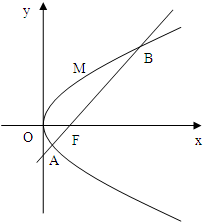 如图,斜率为1的直线过抛物线y2=2px(p>0)的焦点,与抛物线交于两点A、B,M为抛物线弧AB上的动点.
如图,斜率为1的直线过抛物线y2=2px(p>0)的焦点,与抛物线交于两点A、B,M为抛物线弧AB上的动点. 如图,斜率为1的直线过抛物线Ω:y2=2px(p>0)的焦点F,与抛物线交于两点A,B,
如图,斜率为1的直线过抛物线Ω:y2=2px(p>0)的焦点F,与抛物线交于两点A,B, 如图,斜率为1的直线过抛物线y2=2px(p>0)的焦点,与抛物线交于两点A、B,将直线AB按向量
如图,斜率为1的直线过抛物线y2=2px(p>0)的焦点,与抛物线交于两点A、B,将直线AB按向量 过抛物线
过抛物线 的焦点F,与抛物线交于两点A,B。
的焦点F,与抛物线交于两点A,B。 的方程;
的方程; 的面积S的最大值;
的面积S的最大值;