题目内容
 如图,斜率为1的直线过抛物线Ω:y2=2px(p>0)的焦点F,与抛物线交于两点A,B,
如图,斜率为1的直线过抛物线Ω:y2=2px(p>0)的焦点F,与抛物线交于两点A,B,(1)若|AB|=8,求抛物线Ω的方程;
(2)设C为抛物线弧AB上的动点(不包括A,B两点),求△ABC的面积S的最大值;
(3)设P是抛物线Ω上异于A,B的任意一点,直线PA,PB分别交抛物线的准线于M,N两点,证明M,N两点的纵坐标之积为定值(仅与p有关)
分析:(1)由题意得出直线的方程,与抛物线的方程联立,再利用根与系数的关系及抛物线的定义即可求出其方程;
(2)当过点C的切线与AB平行时三角形ABC的面积最大,求出弦长|AB|及两平行线间的距离即可;
(3)根据点A、B、P在抛物线上可设出其坐标,利用点斜式分别写出直线PA、PB的方程,进而得出点M、N的坐标,再利用(1)的结论及根与系数的关系即可证明结论.
(2)当过点C的切线与AB平行时三角形ABC的面积最大,求出弦长|AB|及两平行线间的距离即可;
(3)根据点A、B、P在抛物线上可设出其坐标,利用点斜式分别写出直线PA、PB的方程,进而得出点M、N的坐标,再利用(1)的结论及根与系数的关系即可证明结论.
解答:解:(1)设A(x1,y1),B(x2,y2).
∵直线l斜率为1且过焦点F(
,0),∴直线l的方程为y=x-
.
联立
,消去y得到关于x的方程x2-3px+
=0,
由题意,△=9p2-p2>0.
由根与系数的关系得x1+x2=3p,x1x2=
.
由抛物线的定义可得:|AB|=xx1+x2+p=4p,又|AB|=8,∴4p=8,∴p=2.
因此所求的抛物线方程为y2=4x.
(2)由题意可知:当过点C的切线与AB平行时三角形ABC的面积最大,
设此切线为y=x+t,与抛物线方程联立得
,消去y得到关于x的方程x2+(2t-2p)x+t2=0,
∴△=(2tt-2p)2-4t2=0,解得t=
,∴切线为y=x+
.
因此切线与直线AB的距离d=
=
.
∴△ABC的最大面积=
×
×4p=
p2.
(3)设A(
,y1),B(
,y2),P(
,y0).
则直线PA的方程为y-y0=
(x-
),化为y-y0=
(x-
),
令x=-
,则yM=
,
同理可得yN=
,
∴yM•yN=
,
由(1)可得:y2-2py-p2=0,
∴y1+y2=2p,y1y2=-p2.
∴yM•yN=
=-p2为定值.
∵直线l斜率为1且过焦点F(
| p |
| 2 |
| p |
| 2 |
联立
|
| p2 |
| 4 |
由题意,△=9p2-p2>0.
由根与系数的关系得x1+x2=3p,x1x2=
| p2 |
| 4 |
由抛物线的定义可得:|AB|=xx1+x2+p=4p,又|AB|=8,∴4p=8,∴p=2.
因此所求的抛物线方程为y2=4x.
(2)由题意可知:当过点C的切线与AB平行时三角形ABC的面积最大,
设此切线为y=x+t,与抛物线方程联立得
|
∴△=(2tt-2p)2-4t2=0,解得t=
| p |
| 2 |
| p |
| 2 |
因此切线与直线AB的距离d=
|-
| ||||
|
| ||
| 2 |
∴△ABC的最大面积=
| 1 |
| 2 |
| ||
| 2 |
| 2 |
(3)设A(
| y12 |
| 2p |
| y22 |
| 2p |
| y02 |
| 2p |
则直线PA的方程为y-y0=
| y0-y1 | ||||
|
| y02 |
| 2p |
| 2p |
| y0+y1 |
| y02 |
| 2p |
令x=-
| p |
| 2 |
| y0y1-p2 |
| y0+y1 |
同理可得yN=
| y0y2-p2 |
| y0+y2 |
∴yM•yN=
| y02y1y2-p2y0(y1+y2)+p4 |
| y02+y0(y1+y2)+y1y2 |
由(1)可得:y2-2py-p2=0,
∴y1+y2=2p,y1y2=-p2.
∴yM•yN=
| -y02p2-2p3y0+p4 |
| y02+2py0-p2 |
点评:熟练掌握直线的点斜式方程、抛物线的定义、直线与抛物线方程联立消去一个未知数后得到的一元二次方程的根与系数的关系、切线的性质及两平行线间的距离是解题的关键.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
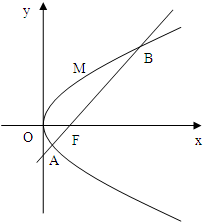 如图,斜率为1的直线过抛物线y2=2px(p>0)的焦点,与抛物线交于两点A、B,M为抛物线弧AB上的动点.
如图,斜率为1的直线过抛物线y2=2px(p>0)的焦点,与抛物线交于两点A、B,M为抛物线弧AB上的动点. 如图,斜率为1的直线过抛物线y2=2px(p>0)的焦点,与抛物线交于两点A、B,将直线AB按向量
如图,斜率为1的直线过抛物线y2=2px(p>0)的焦点,与抛物线交于两点A、B,将直线AB按向量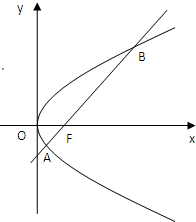 如图,斜率为1的直线过抛物线y2=2px(p>0)的焦点,与抛物线交于两点A、B,将直线AB按向量
如图,斜率为1的直线过抛物线y2=2px(p>0)的焦点,与抛物线交于两点A、B,将直线AB按向量 过抛物线
过抛物线 的焦点F,与抛物线交于两点A,B。
的焦点F,与抛物线交于两点A,B。 的方程;
的方程; 的面积S的最大值;
的面积S的最大值;