题目内容
【题目】已知椭圆![]() 的离心率为
的离心率为![]() , 倾斜角为
, 倾斜角为![]() 的直线
的直线![]() 经过椭圆
经过椭圆![]() 的右焦点且与圆
的右焦点且与圆![]() 相切.
相切.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与圆
与圆![]() 相切于点
相切于点![]() , 且交椭圆
, 且交椭圆![]() 于
于![]() 两点,射线
两点,射线![]() 于椭圆
于椭圆![]() 交于点
交于点![]() ,设
,设![]() 的面积与
的面积与![]() 的面积分别为
的面积分别为![]() .
.
①求![]() 的最大值; ②当
的最大值; ②当![]() 取得最大值时,求
取得最大值时,求![]() 的值.
的值.
【答案】(1)![]() ; (2)
; (2)![]() .
.
【解析】
(1)根据已知得到a,b,c的方程,解方程组即得椭圆的标准方程.(2) ①先把直线和椭圆的方程联立计算出![]() ,再计算出弦长|AB|和
,再计算出弦长|AB|和![]() ,即得
,即得![]() 的最大值;②先计算出
的最大值;②先计算出![]() ,
,![]() 最后计算
最后计算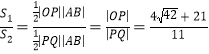 .
.
(1)依题直线![]() 的斜率
的斜率![]() .设直线
.设直线![]() 的方程为
的方程为![]() ,
,
依题有: 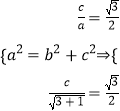
(2)由直线![]() 与圆
与圆![]() 相切得:
相切得: ![]() .
.
设![]() .将直线
.将直线![]() 代入椭圆
代入椭圆![]() 的方程得:
的方程得:
![]()
![]()
![]() 且
且 ![]() .
.
![]()
![]()
设点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,故
,故![]() 的面积为:
的面积为:
![]() ,
,
当![]() .等号成立.故
.等号成立.故![]() 的最大值为1.
的最大值为1.
设![]() ,由直线
,由直线![]() 与圆
与圆![]() 相切于点
相切于点![]() ,可得
,可得![]() ,
,
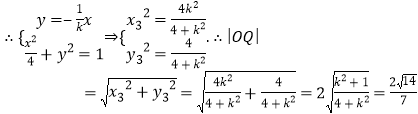 .
.
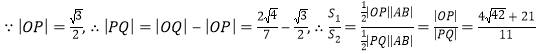 .
.

练习册系列答案
相关题目

