题目内容
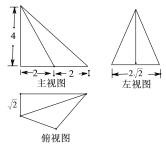
【题目】某几何体的三视图如图所示,则该几何体的外接球的表面积为_____.
【答案】![]()
【解析】
作出几何体的直观图,建立空间直角坐标系,求出外接球的球心坐标,从而可得外接球的半径,再计算出外接球的表面积.
由三视图可知几何体为四棱锥E﹣ABCD,直观图如图所示:
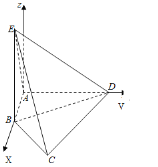
其中,BE⊥平面ABCD,BE=4,AB⊥AD,AB=![]() ,
,
C到AB的距离为2,C到AD的距离为2![]() ,
,
以A为原点,以AB,AD,及平面ABCD过A的垂线为坐标轴建立空间直角坐标系A﹣xyz,
则A(0,0,0),B(![]() ,0,0),C(2
,0,0),C(2![]() ,2,0),D(0,4,0),E(
,2,0),D(0,4,0),E(![]() ,0,4).
,0,4).
设外接球的球心为M(x,y,z),则MA=MB=MC=MD=ME,
∴x2+y2+z2=y2+(x﹣![]() )2+z2=(y﹣2)2+(x﹣2
)2+z2=(y﹣2)2+(x﹣2![]() )2+z2=(y﹣4)2+x2+z2=y2+(x﹣
)2+z2=(y﹣4)2+x2+z2=y2+(x﹣![]() )2+(z﹣4)2,
)2+(z﹣4)2,
解得y=2,x=![]() ,z=2.
,z=2.
∴外接球的半径r=MA=![]() =
=![]() ,
,
∴外接球的表面积S=4πr2=34π.
故答案为:34π

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目