题目内容
在R上定义运算?:x?y=x(1-y).若方程1?(2-kx)=-
有解,则k的取值范围是( )
| -x2+4x-3 |
分析:根据运算?:x?y=x(1-y),把1?(2-kx)=-
,转化为kx-1=-
在[1,3]有解,讨论两边对应的函数的取值即可求得结果.
| -x2+4x-3 |
| -x2+4x-3 |
解答:解:∵x?y=x(1-y),
∴1?(2-kx)=-
?kx-1=-
即-kx+1=
两边平方,整理得:
方程组在区间[1,3]上有解,讨论它的图象可得0≤k≤1.
故选B.
∴1?(2-kx)=-
| -x2+4x-3 |
| -x2+4x-3 |
| -x2+4x-3 |
两边平方,整理得:
|
方程组在区间[1,3]上有解,讨论它的图象可得0≤k≤1.
故选B.
点评:题的难点在于能否对于给定的定义理解透彻,也是此题新意,能有效考查学生灵活应用知识分析、解决问题的能力.这个的立意很好,属中档题.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 :x
:x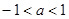 B.0<
B.0< <2 C.
<2 C. D.
D.
 :x
:x B.
B. C.
C. D.
D.