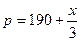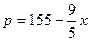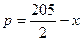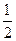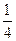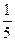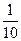题目内容
(本小题满分12分)
某柑桔基地因冰雪灾害,使得果林严重受损,为此有关专家提出两种拯救果林的方案,每种方案都需分两年实施;若实施方案一,预计当年可以使柑桔产量恢复到灾前的1.0倍、0.9倍、0.8倍的概率分别是0.3、0.3、0.4;第二年可以使柑桔产量为上一年产量的1.25倍、1.0倍的概率分别是0.5、0.5. 若实施方案二,预计当年可以使柑桔产量达到灾前的1.2倍、1.0倍、0.8倍的概率分别是0.2、0.3、0.5;第二年可以使柑桔产量为上一年产量的1.2倍、1.0倍的概率分别是0.4、0.6. 实施每种方案,第二年与第一年相互独立。令 表示方案
表示方案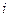 实施两年后柑桔产量达到灾前产量的倍数。
实施两年后柑桔产量达到灾前产量的倍数。
(1)写出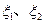 的分布列;
的分布列;
(2)实施哪种方案,两年后柑桔产量超过灾前产量的概率更大?
(3)不管哪种方案,如果实施两年后柑桔产量达不到灾前产量,预计可带来效益10万元;两年后柑桔产量恰好达到灾前产量,预计可带来效益15万元;柑桔产量超过灾前产量,预计可带来效益20万元;问实施哪种方案所带来的平均效益更大?
某柑桔基地因冰雪灾害,使得果林严重受损,为此有关专家提出两种拯救果林的方案,每种方案都需分两年实施;若实施方案一,预计当年可以使柑桔产量恢复到灾前的1.0倍、0.9倍、0.8倍的概率分别是0.3、0.3、0.4;第二年可以使柑桔产量为上一年产量的1.25倍、1.0倍的概率分别是0.5、0.5. 若实施方案二,预计当年可以使柑桔产量达到灾前的1.2倍、1.0倍、0.8倍的概率分别是0.2、0.3、0.5;第二年可以使柑桔产量为上一年产量的1.2倍、1.0倍的概率分别是0.4、0.6. 实施每种方案,第二年与第一年相互独立。令
 表示方案
表示方案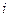 实施两年后柑桔产量达到灾前产量的倍数。
实施两年后柑桔产量达到灾前产量的倍数。(1)写出
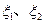 的分布列;
的分布列;(2)实施哪种方案,两年后柑桔产量超过灾前产量的概率更大?
(3)不管哪种方案,如果实施两年后柑桔产量达不到灾前产量,预计可带来效益10万元;两年后柑桔产量恰好达到灾前产量,预计可带来效益15万元;柑桔产量超过灾前产量,预计可带来效益20万元;问实施哪种方案所带来的平均效益更大?
(1)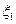 、
、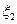 的分布列分别为:
的分布列分别为:
(2)方案二两年后柑桔产量超过灾前产量的概率更大。
(3)方案一所带来的平均效益更大。
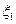 、
、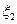 的分布列分别为:
的分布列分别为: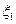 | 0.8 | 0.9 | 1.0 | 1.125 | 1.25 |
| P | 0.2 | 0.15 | 0.35 | 0.15 | 0.15 |
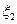 | 0.8 | 0.96 | 1.0 | 1.2 | 1.44 |
| P | 0.3 | 0.2 | 0.18 | 0.24 | 0.08 |
(2)方案二两年后柑桔产量超过灾前产量的概率更大。
(3)方案一所带来的平均效益更大。
(1)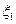 的所有取值为
的所有取值为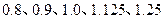
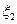 的所有取值为
的所有取值为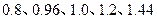 ,
,
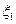 、
、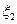 的分布列分别为:
的分布列分别为:
(2)令A、B分别表示方案一、方案二两年后柑桔产量超过灾前产量这一事件,
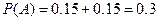 ,
,
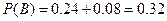 ,
,
可见,方案二两年后柑桔产量超过灾前产量的概率更大。
(3)令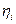 表示方案
表示方案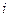 所带来的效益,则
所带来的效益,则
所以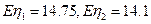 ,
,
可见,方案一所带来的平均效益更大。
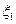 的所有取值为
的所有取值为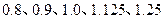
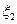 的所有取值为
的所有取值为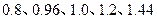 ,
,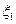 、
、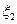 的分布列分别为:
的分布列分别为: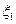 | 0.8 | 0.9 | 1.0 | 1.125 | 1.25 |
| P | 0.2 | 0.15 | 0.35 | 0.15 | 0.15 |
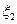 | 0.8 | 0.96 | 1.0 | 1.2 | 1.44 |
| P | 0.3 | 0.2 | 0.18 | 0.24 | 0.08 |
(2)令A、B分别表示方案一、方案二两年后柑桔产量超过灾前产量这一事件,
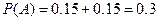 ,
,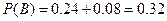 ,
,可见,方案二两年后柑桔产量超过灾前产量的概率更大。
(3)令
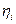 表示方案
表示方案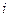 所带来的效益,则
所带来的效益,则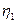 | 10 | 15 | 20 |
| P | 0.35 | 0.35 | 0.3 |
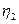 | 10 | 15 | 20 |
| P | 0.5 | 0.18 | 0.32 |
所以
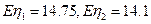 ,
,可见,方案一所带来的平均效益更大。

练习册系列答案
相关题目
 统计信息
统计信息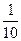
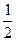
 (万元),求
(万元),求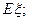
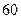 名学生,将其数学成绩(均为整数)分成六段
名学生,将其数学成绩(均为整数)分成六段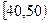 ,
,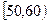 …
…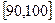 后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
后得到如下部分频率分布直方图.观察图形的信息,回答下列问题: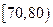 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;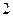 人,抽到的学生成绩在
人,抽到的学生成绩在 记
记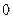 分,在
分,在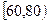 记
记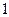 分,在
分,在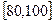 记
记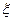 表示抽取结束后的总记分,求
表示抽取结束后的总记分,求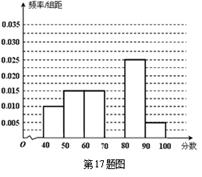
 商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费每满100元可以转动如图所示的圆盘一
商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费每满100元可以转动如图所示的圆盘一 次,其中O为圆心,且标有20元、10元、0元的三部分区域面积相等,假定指针停在任一位置都是等可能的.当指针停在某区域时,返相应金额的优惠券。(例如:某顾客消费了218元,第一次转动获得了20元,第二次获得了10元,则其共获得了30元优惠券。)顾客甲和乙都到商场进行了消费,并按照规则参与了活动.
次,其中O为圆心,且标有20元、10元、0元的三部分区域面积相等,假定指针停在任一位置都是等可能的.当指针停在某区域时,返相应金额的优惠券。(例如:某顾客消费了218元,第一次转动获得了20元,第二次获得了10元,则其共获得了30元优惠券。)顾客甲和乙都到商场进行了消费,并按照规则参与了活动. 得优惠券面额大于0元的概率?
得优惠券面额大于0元的概率?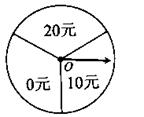
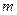 和
和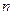 ,向量
,向量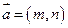 与向量
与向量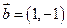 的夹角为
的夹角为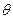 ,则
,则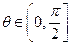 的概率是
的概率是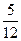
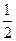
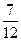
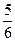
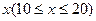 万件的该种产品所需要的总成本为
万件的该种产品所需要的总成本为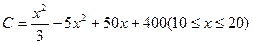 万元,市场销售情况可能出现好、中、差三种情况,各种情况发生的概率和相应的价格p(元)与年产量x之间的函数关系如下表所示.
万元,市场销售情况可能出现好、中、差三种情况,各种情况发生的概率和相应的价格p(元)与年产量x之间的函数关系如下表所示.