题目内容
20.已知点M(x,y)满足条件$\left\{\begin{array}{l}{\underset{x-y+2≥0}{x+y-4≥0}}\\{2x-y-5≤0}\end{array}\right.$,点N(x,y)满足x2+y2-10y+23≤0,则|MN|的最小值为$\frac{\sqrt{2}}{2}$.分析 分别作出不等式组对应的平面区域,利用点到直线的距离公式进行求解即可.
解答 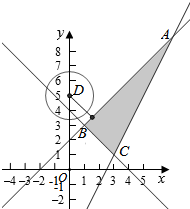 解:由x2+y2-10y+23≤0得x2+(y-5)2≤2,对应的图象以D(0,5)为圆心,半径r=$\sqrt{2}$的圆及其内部,
解:由x2+y2-10y+23≤0得x2+(y-5)2≤2,对应的图象以D(0,5)为圆心,半径r=$\sqrt{2}$的圆及其内部,
作出不等式组对应的平面区域如图:
则圆心D到直线x-y+2=0的距离d=$\frac{|0-5+2|}{\sqrt{2}}=\frac{3}{\sqrt{2}}$=$\frac{3\sqrt{2}}{2}$,
此时|MN|的最小值d-r=$\frac{3\sqrt{2}}{2}$-$\sqrt{2}$=$\frac{\sqrt{2}}{2}$,
故答案为:$\frac{\sqrt{2}}{2}$
点评 本题主要考查线性规划的应用,作出不等式组对应的平面区域利用数形结合是解决本题的关键.

练习册系列答案
相关题目
5.若实数x,y满足$\left\{\begin{array}{l}{x-y≤0}\\{x+y-4≤0}\\{x≥0}\end{array}\right.$,则|3x+y-4|+|x+2y+8|的最小值是( )
| A. | 11 | B. | 12 | C. | 16 | D. | 18 |
10.设集合A=B={(x,y)|x,y∈R},f是A到B的一个映射,且满足f:(x,y)→(xy,x-y),若集合B中的元素(a,b)在集合A中只有唯一的元素与之对应,则a,b应满足的关系式为( )
| A. | b2-2a=0 | B. | b2+4a=0 | C. | b2+2a=0 | D. | b2-4a=0 |