题目内容
16.已知函数f(x)=x2ekx.(Ⅰ)当k=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)设g(x)=$\frac{ax}{1+{x}^{2}}$+2(a>0),且对于任意的x1,x2∈[0,2],均有g(x1)≥f(x2)恒成立,求实数k的取值范围.
分析 (1)求出k=1时f(x)的导数,求得切点,由点斜式方程即可得到切线方程;
(2)“对任意的x1,x2∈[0,2],f(x1)≥g(x2)恒成立”等价于“当a>0时,对任意的x1,x2∈[0,2],gmin(x)≥fmax(x)成立”,求得g(x)在[0,2]上的最小值,再求f(x)的导数,对k讨论,结合单调性,求得最大值,解不等式即可得到.
解答 解:(1)当k=1时,f(x)=x2ex.的导数为f′(x)=(x2+2x)ex,
f(1)=e,切线的斜率为f′(1)=3e,
即有切线方程为y-e=3e(x-1),即3ex-y-2e=0;
(2)“任意的x1,x2∈[0,2],均有g(x1)≥f(x2)恒成立”
等价于“当a>0时,对任意的x1,x2∈[0,2],gmin(x)≥fmax(x)成立”,
当a>0时,函数g(x)在[0,1]上单调递增,在[1,2]上单调递减,
而g(0)=2,g(2)=$\frac{2a}{5}$+2,所以g(x)的最小值为g(0)=2,
f(x)的导数f′(x)=2xekx+x2ekx•k=(kx2+2x)ekx,
当k=0时,f(x)=x2,x∈[0,2]时,fmax(x)=f(2)=4,显然不满足fmax(x)≤1,
当k≠0时,令f′(x)=0得,x1=0,x2=-$\frac{2}{k}$,
①当-$\frac{2}{k}$≥2,即-1≤k≤0时,在[0,2]上f′(x)≥0,所以f(x)在[0,2]单调递增,
所以fmax(x)=f(2)=4e2k,只需4e2k≤1,得k≤-ln2,所以-1≤k≤-ln2;
②当0<-$\frac{2}{k}$<2,即k<-1时,在[0,-$\frac{2}{k}$],f(x)单调递增,
在[-$\frac{2}{k}$,2],f(x)单调递减,所以fmax(x)=f(-$\frac{2}{k}$)=$\frac{4}{{k}^{2}{e}^{2}}$,
只需$\frac{4}{{k}^{2}{e}^{2}}$≤1,得k≤-$\frac{2}{e}$,所以k<-1;
③当-$\frac{2}{k}$<0,即k>0时,显然在[0,2]上f′(x)≥0,f(x)单调递增,
fmax(x)=f(2)=4e2k,4e2k≤1不成立.
综上所述,k的取值范围是(-∞,-ln2].
点评 本题考查导数的运用:求切线方程和单调区间、极值和最值,主要考查不等式的恒成立问题转化为求函数最值,运用分类讨论的思想方法是解题的关键.

| A. | 8 | B. | 12 | C. | 16 | D. | 20 |
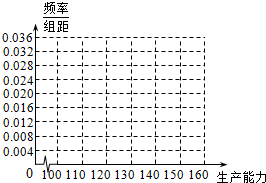 某工厂有工人1000名,其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人).现用分层抽样方法(按A类、B类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(此处生产能力指一天加工的零件数).
某工厂有工人1000名,其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人).现用分层抽样方法(按A类、B类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(此处生产能力指一天加工的零件数).从A类工人中的抽查结果和从B类工人中的抽查结果分别如表1和表2.
表1:
| 生产能 力分组 | [100,110) | [110,120) | [120,130) | [130,140) | [140,150) |
| 人数 | 4 | 8 | x | 5 | 3 |
| 生产能 力分组 | [110,120) | [120,130) | [130,140) | [140,150) |
| 人数 | 6 | y | 36 | 18 |

| A. | 2 | B. | -1 | C. | 4 | D. | 2015 |
 已知函数f(x)=$\left\{\begin{array}{l}{(\frac{1}{2})^{x-1},x>1}\\{{x}^{2},x≤1}\end{array}\right.$.
已知函数f(x)=$\left\{\begin{array}{l}{(\frac{1}{2})^{x-1},x>1}\\{{x}^{2},x≤1}\end{array}\right.$.