题目内容
【题目】某高校为了对2018年录取的大一理工科新生有针对性地进行教学，从大一理工科新生中随机抽取40名，对他们2018年高考的数学分数进行分析，研究发现这40名新生的数学分数
在
内，且其频率
满足
（其中
，
）.
（1）求
的值；
（2）请画出这20名新生高考数学分数的频率分布直方图，并估计这40名新生的高考数学分数的平均数（同一组中的数据用该组区间的中点值作代表）；
（3）将此样本的频率估计为总体的概率，随机调查4名该校的大一理工科新生，记调查的4名大一理工科新生中“高考数学分数不低于130分”的人数为随机变量，求的数学期望.
【答案】（1）
;(2)120;(3)见解析.
【解析】
（1）由题意知：
，所以的取值为10，11，12，13，14，
代入
，由频率和等于1可求
的值；
（2）由（1），得
，可得频率分布直方图如图：
3）由题意可知，
，且“高考数学分数不低于130分”的概率为
，所以
～
，可求的数学期望.
（1）由题意知：，所以的取值为10，11，12，13，14，
代入，可得
，
解得.
（2）由（1），得，频率分布直方图如图：
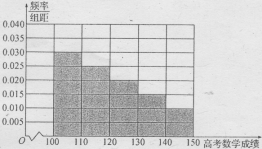
这40名新生的高考数学分数的平均数为
.
（3）由题意可知，，且“高考数学分数不低于130分”的概率为，所以～
所以
.
练习册系列答案
相关题目
