题目内容
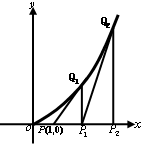 (2013•韶关二模)如图,过点P(1,0)作曲线C:y=x2(x∈(0,+∞))的切线,切点为Q1,设点Q1在x轴上的投影是点P1;又过点P1作曲线C的切线,切点为Q2,设Q2在x轴上的投影是P2;…;依此下去,得到一系列点Q1,Q2,Q3-Qn,设点Qn的横坐标为an.
(2013•韶关二模)如图,过点P(1,0)作曲线C:y=x2(x∈(0,+∞))的切线,切点为Q1,设点Q1在x轴上的投影是点P1;又过点P1作曲线C的切线,切点为Q2,设Q2在x轴上的投影是P2;…;依此下去,得到一系列点Q1,Q2,Q3-Qn,设点Qn的横坐标为an.(1)求直线PQ1的方程;
(2)求数列{an}的通项公式;
(3)记Qn到直线PnQn+1的距离为dn,求证:n≥2时,
| 1 |
| d1 |
| 1 |
| d2 |
| 1 |
| dn |
分析:(1)求出函数的导数,利用斜率相等,求出a1,然后求直线PQ1的方程;
(2)通过求解函数的导数与切线的斜率,判断数列{an}是等差数列,然后求出它的通项公式;
(3)利用Qn到直线PnQn+1的距离为dn,通过公式利用基本不等式,即可通过累加法证明n≥2时,
+
+…
>3.
(2)通过求解函数的导数与切线的斜率,判断数列{an}是等差数列,然后求出它的通项公式;
(3)利用Qn到直线PnQn+1的距离为dn,通过公式利用基本不等式,即可通过累加法证明n≥2时,
| 1 |
| d1 |
| 1 |
| d2 |
| 1 |
| dn |
解答:解:(1)令Q1(a1,a12),由y′=2x得kPQ1=2x1…(1分)
即
=2a1 故a1=2…(2分)
∴kQP=4,则切线l1的方程为:4x-y-4=0…(4分)
(2)令Qn(an,an2),则Qn-1(an-1,an-12),Pn-1(an-1,0),
∴KPn-1Qn=
=2an…(5分)
化简得
=2,(n≥2),…(6分)
故数列{an}是以2为首项2为公比的等比数列…(7分)
所以an=2n…(9分)
(3)由(2)知Pn-1(2n,0),Qn-1(2n+1,22n+2),Qn(2n,22n),
故KPnQn+1=
=2n+2,∴lPnQn+1:2n+2x-y-22n+2=0…(10分)
∴dn=
=
<
=
.…(11分)
∴
>
…(12分)
故
+
+…
>4[
+(
)2+…+(
)n]=4×
=4[1-(
)n]>4>3.…(14分)
即
| ||
| a1-1 |
∴kQP=4,则切线l1的方程为:4x-y-4=0…(4分)
(2)令Qn(an,an2),则Qn-1(an-1,an-12),Pn-1(an-1,0),
∴KPn-1Qn=
| ||
| an-an-1 |
化简得
| an |
| an-1 |
故数列{an}是以2为首项2为公比的等比数列…(7分)
所以an=2n…(9分)
(3)由(2)知Pn-1(2n,0),Qn-1(2n+1,22n+2),Qn(2n,22n),
故KPnQn+1=
| 22n+2-0 |
| 2n+1-2n |
∴dn=
| |2n+2•2n-22n-22n+2| | ||
|
| 4n | ||
|
| 4n |
| 4•2n |
| 2n |
| 4 |
∴
| 1 |
| dn |
| 4 |
| 2n |
故
| 1 |
| d1 |
| 1 |
| d2 |
| 1 |
| dn |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||||
1-
|
| 1 |
| 2 |
点评:本题考查数列与函数的综合应用,函数的导数与直线的切线的关系,点到直线的距离公式的应用,基本不等式以及累加法证明不等式的方法,考查计算能力.

练习册系列答案
相关题目