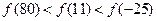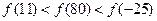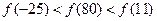题目内容
已知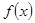 是R上的偶函数,且在区间
是R上的偶函数,且在区间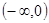 上是增函数,若
上是增函数,若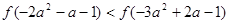 ,那么实数
,那么实数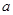 的取值范围是( )
的取值范围是( )
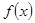 是R上的偶函数,且在区间
是R上的偶函数,且在区间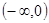 上是增函数,若
上是增函数,若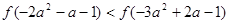 ,那么实数
,那么实数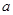 的取值范围是( )
的取值范围是( )| A.(-1,0) | B.(-∞,0)∪(3,+∞) | C.(3,+∞) | D.(0,3) |
D
分析:利用函数的单调性,将函数值的大小关系转化为自变量的关系得出关于a的不等式是解决本题的关键,还要注意整体自变量的取值是否属于该定义区间.
解:由于-2a2-a-1=-2((a+
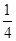 )2+
)2+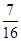 )<0,-3a2+2a-1=-3((a-
)<0,-3a2+2a-1=-3((a-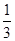 )2+
)2+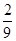 )<0,
)<0,故-2a2-a-1,-3a2+2a-1均在区间(-∞,0)上,
因此f(-2a2-a-1)<f(-3a2+2a-1)?-2a2-a-1<-3a2+2a-1,
解得a∈(0,3).
故选D.

练习册系列答案
相关题目
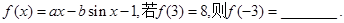
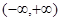 上的偶函数
上的偶函数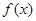 满足
满足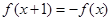 ,且
,且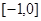 上是增函数,下面五个关于
上是增函数,下面五个关于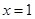 对称;③
对称;③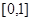 上是增函数;④
上是增函数;④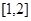 上为减函数;⑤
上为减函数;⑤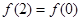 ,正确命题的个数是 ( )
,正确命题的个数是 ( )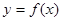 在区间[3,7]上是增函数,且最小值为-5,那么
在区间[3,7]上是增函数,且最小值为-5,那么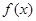 在区间[-7,-3]
在区间[-7,-3]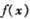 满足
满足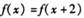 ,当
,当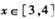 时
时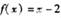 ,则
,则

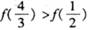
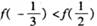
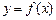 是奇函数,当
是奇函数,当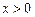 时,
时,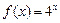 则
则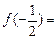 .
.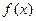 和偶函数
和偶函数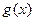 满足
满足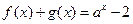 ,
,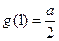 ,则
,则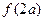 等于 .
等于 . 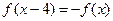 ,且在区间[0,2]上是增函数,则( )
,且在区间[0,2]上是增函数,则( )