题目内容
【题目】已知圆![]() (
(![]() 为坐标原点),直线
为坐标原点),直线![]() .
.
(1)过直线![]() 上任意一点
上任意一点![]() 作圆
作圆![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,求四边形
,求四边形![]() 面积的最小值.
面积的最小值.
(2)过点![]() 的直线
的直线![]() 分别与圆
分别与圆![]() 交于点
交于点![]() (
(![]() 不与
不与![]() 重合),若
重合),若![]() ,试问直线
,试问直线![]() 是否过定点?并说明理由.
是否过定点?并说明理由.
【答案】(1)12;(2)过定点,理由见解析
【解析】
(1)由![]() ,得过点
,得过点![]() 的切线长
的切线长![]() ,所以四边形
,所以四边形![]() 的面积为
的面积为![]() ,即可得到本题答案;
,即可得到本题答案;
(2)设直线![]() 的方程为
的方程为![]() ,则直线
,则直线![]() 的方程为
的方程为![]() .
.
联立方程 ,消去
,消去![]() ,整理得
,整理得![]() ,
,
得 ,
,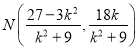 ,
,
所以 ,令
,令![]() ,即可得到本题答案.
,即可得到本题答案.
(1)由题意可得圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,从而
,从而![]() ,
,
则过点![]() 的切线长
的切线长![]() .
.
故四边形![]() 的面积为
的面积为![]() ,即四边形
,即四边形![]() 面积的最小值为12.
面积的最小值为12.
(2)因为![]() ,所以直线
,所以直线![]() 与直线
与直线![]() 的斜率都存在,且不为0.
的斜率都存在,且不为0.
设直线![]() 的方程为
的方程为![]() ,则直线
,则直线![]() 的方程为
的方程为![]() .
.
联立方程 ,消去
,消去![]() ,整理得
,整理得![]()
解得![]() 或
或![]() ,则
,则 .
.
同理可得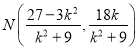 .
.
所以 .
.
令![]() ,得
,得![]() ,解得
,解得![]() .
.
取![]() ,可以证得
,可以证得![]() ,所以直线
,所以直线![]() 过定点
过定点![]() .
.
当![]() 时,
时,![]() 轴,易知
轴,易知![]() 与
与![]() 均为正三角形,直线
均为正三角形,直线![]() 的方程为
的方程为![]() ,也过定点
,也过定点![]() .
.
综上,直线![]() 过定点
过定点![]() .
.

【题目】海水受日月的引力,在一定的时候发生涨落的现象叫潮,一般地,早潮叫潮,晚潮叫汐.在通常情况下,船在涨潮时驶进航道,靠近码头;卸货后,在落潮时返回海洋.下面是某港口在某季节每天的时间与水深关系表:
时刻 | 2:00 | 5:00 | 8:00 | 11:00 | 14:00 | 17:00 | 20:00 | 23:00 |
水深(米) | 7.5 | 5.0 | 2.5 | 5.0 | 7.5 | 5.0 | 2.5 | 5.0 |
经长期观测,这个港口的水深与时间的关系,可近似用函数f(t)=Asin(ωt+)+b![]() 来描述.
来描述.
(1)根据以上数据,求出函数f(t)=Asin(ωt+)+b的表达式;
(2)一条货船的吃水深度(船底与水面的距离)为4.25米,安全条例规定至少要有2米的安全间隙(船底与洋底的距离),该船在一天内(0:00~24:00)何时能进入港口然后离开港口?每次在港口能停留多久?
【题目】“绿水青山就是金山银山”的生态文明发展理念已经深入人心,这将推动新能源汽车产业的迅速发展.下表是2019年我国某地区新能源乘用车的前5个月销售量与月份的统计表:
月份代码 | 1 | 2 | 3 | 4 | 5 |
销售量 | 0.5 | 0.6 | 1 | 1.4 | 1.5 |
(1)利用线性相关系数![]() 判断
判断![]() 与
与![]() 的线性相关性,并求出线性回归方程
的线性相关性,并求出线性回归方程
(2)根据线性回归方程预报2019年6月份的销售量约为多少万辆?
参考公式: ,
,![]() ;回归直线:
;回归直线:![]() .
.
 ,
,![]()