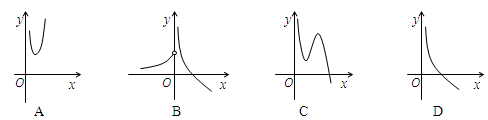题目内容
已知函数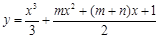 的两个极值点分别为x1,x2,且x1Î(0, 1),x2Î(1, +¥),记分别以m,n为横、纵坐标的点P(m,n)表示的平面区域为D,若函数
的两个极值点分别为x1,x2,且x1Î(0, 1),x2Î(1, +¥),记分别以m,n为横、纵坐标的点P(m,n)表示的平面区域为D,若函数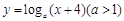 的图象上存在区域D内的点,则实数a的取值范围为( )
的图象上存在区域D内的点,则实数a的取值范围为( )
A.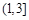 | B.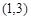 | C. | D.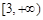 |
B
解析试题分析:因为,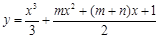 ,所以,y'=x2+mx+
,所以,y'=x2+mx+ (m+n),
(m+n),
依题意知,方程y'=0有两个根x1、x2,且x1∈(0,1),x2∈(1,+∞),
构造函数f(x)=x2+mx+ (m+n),
(m+n),
所以,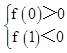 ,即
,即 ,
,
∵直线m+n=0,2+3m+n=0的交点坐标为(-1,1)
∴要使函数y=loga(x+4)(a>1)的图象上存在区域D上的点,则必须满足1>loga(-1+4)
∴loga3<1,解得a<3
又∵a>1,∴1<a<3,故选B.
考点:利用导数研究函数的极值,二元一次不等式(组)与平面区域。
点评:中档题,本题综合性较强,应用导数研究函数的极值,通过构造函数结合函数图象研究方程跟单分布,体现应用数学知识的灵活性。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若 ,则
,则 等于( )
等于( )
A. | B. | C.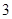 | D. |
函数 在
在 上单调递增,则
上单调递增,则 的最小值为( )
的最小值为( )
| A.1 | B.3 | C.4 | D.9 |
已知函数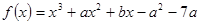 在
在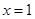 处取得极大值
处取得极大值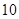 ,则
,则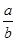 的值为( )
的值为( )
A. | B.-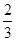 | C.-2或一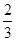 | D.不存在 |
函数 导数是( )
导数是( )
A. | B. |
C.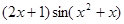 | D. |
曲线 在点
在点 处的切线与坐标轴所围三角形的面积为( )
处的切线与坐标轴所围三角形的面积为( )
A. | B. | C. | D. |
已知实数a,b满足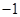 ≤a≤1,
≤a≤1,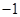 ≤b≤1,则函数
≤b≤1,则函数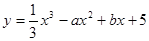 有极值的概率为( )
有极值的概率为( )
A. | B. | C.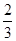 | D.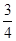 |
函数 的的单调递增区间是 ( )
的的单调递增区间是 ( )
A.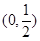 | B.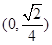 | C.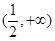 | D. 和 和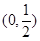 |
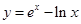 的图象是( )
的图象是( )