题目内容
曲线 在点
在点 处的切线与坐标轴所围三角形的面积为( )
处的切线与坐标轴所围三角形的面积为( )
A. | B. | C. | D. |
D
解析试题分析:欲切线与坐标轴所围成的三角形的面积,只须求出切线在坐标轴上的截距即可,故先利用导数求出在x=2处的导函数值,再结合导数的几何意义即可求出切线的斜率.最后求出切线的方程,从而问题解决.解析:依题意得y′=ex,因此曲线y=ex在点A(2,e2)处的切线的斜率等于e2,相应的切线方程是y-e2=e2(x-2),当x=0时,y=-e2,即y=0时,x=1,∴切线与坐标轴所围成的三角形的面积为: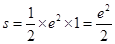 ,故答案为D.
,故答案为D.
考点:线的方程、三角形的面积、导数的几何意义
点评:本小题主要考查直线的方程、三角形的面积、导数的几何意义、利用导数研究曲线上某点切线方程等基础知识,考查运算求解能力.属于基础题.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
若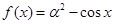 ,则
,则 等于( )
等于( )
A.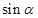 | B. | C.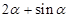 | D. |
若函数 的导函数
的导函数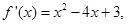 则函数
则函数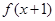 的单调递减区间是( )
的单调递减区间是( )
A.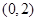 | B.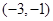 | C.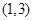 | D.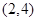 |
已知函数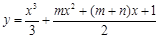 的两个极值点分别为x1,x2,且x1Î(0, 1),x2Î(1, +¥),记分别以m,n为横、纵坐标的点P(m,n)表示的平面区域为D,若函数
的两个极值点分别为x1,x2,且x1Î(0, 1),x2Î(1, +¥),记分别以m,n为横、纵坐标的点P(m,n)表示的平面区域为D,若函数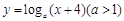 的图象上存在区域D内的点,则实数a的取值范围为( )
的图象上存在区域D内的点,则实数a的取值范围为( )
A.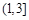 | B.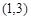 | C. | D.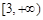 |
已知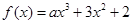 ,若
,若 ,则a的值等于 ( )
,则a的值等于 ( )
A.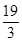 | B. | C.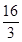 | D.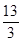 |
已知点 在曲线
在曲线 上,
上, 为曲线在点
为曲线在点 处的切线的倾斜角,则
处的切线的倾斜角,则 取值范围是
取值范围是
A.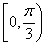 | B. | C.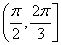 | D. |
函数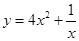 的单调递增区间为( )
的单调递增区间为( )
A.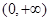 | B. | C. | D.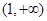 |
已知函数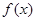 是定义在
是定义在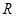 上的可导函数,且
上的可导函数,且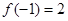 ,
, ,则不等式
,则不等式 的解集为
的解集为
A.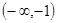 | B. | C. | D. |
定义在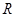 上的可导函数
上的可导函数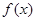 ,当
,当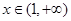 时,
时,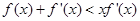 恒成立,
恒成立,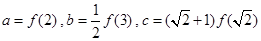 ,则
,则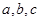 的大小关系为 ( )
的大小关系为 ( )
A.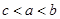 | B.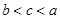 | C.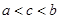 | D. |