题目内容
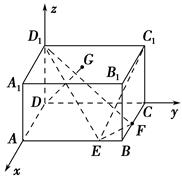
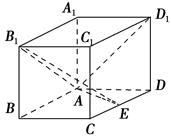
如图,在长方体ABCDA1B1C1D1中,已知AB=4,AD=3,AA1=2,E,F分别是棱AB,BC上的点,且EB=FB=1.
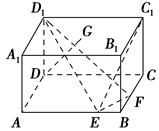
(1)求异面直线EC1与FD1所成角的余弦值;
(2)试在面A1B1C1D1上确定一点G,使DG⊥平面D1EF.

(1)求异面直线EC1与FD1所成角的余弦值;
(2)试在面A1B1C1D1上确定一点G,使DG⊥平面D1EF.
(1)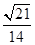 (2)当点G在面A1B1C1D1上,且到A1D1,C1D1距离均为
(2)当点G在面A1B1C1D1上,且到A1D1,C1D1距离均为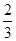 时,DG⊥D1EF.
时,DG⊥D1EF.
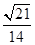 (2)当点G在面A1B1C1D1上,且到A1D1,C1D1距离均为
(2)当点G在面A1B1C1D1上,且到A1D1,C1D1距离均为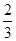 时,DG⊥D1EF.
时,DG⊥D1EF.(1)以D为原点,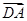 ,
,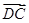 ,
,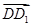 分别为x轴,y轴,z轴的正向建立空间直角坐标系,
分别为x轴,y轴,z轴的正向建立空间直角坐标系,
则有D(0,0,0),D1(0,0,2),C1(0,4,2),E(3,3,0),F(2,4,0),
于是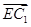 =(-3,1,2),
=(-3,1,2),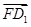 =(-2,-4,2).
=(-2,-4,2).
设EC1与FD1所成角为α,则cos α=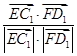 =
=

∴异面直线EC1与FD1所成角的余弦值为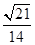 .
.
(2)因点G在平面A1B1C1D1上,故可设G(x,y,2).
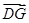 =(x,y,2),
=(x,y,2),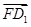 =(-2,-4,2),
=(-2,-4,2),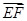 =(-1,1,0).由
=(-1,1,0).由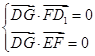
得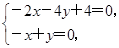 解得
解得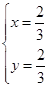
故当点G在面A1B1C1D1上,且到A1D1,C1D1距离均为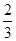 时,DG⊥D1EF
时,DG⊥D1EF
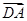 ,
,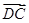 ,
,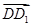 分别为x轴,y轴,z轴的正向建立空间直角坐标系,
分别为x轴,y轴,z轴的正向建立空间直角坐标系,
则有D(0,0,0),D1(0,0,2),C1(0,4,2),E(3,3,0),F(2,4,0),
于是
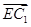 =(-3,1,2),
=(-3,1,2),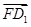 =(-2,-4,2).
=(-2,-4,2).设EC1与FD1所成角为α,则cos α=
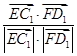 =
=
∴异面直线EC1与FD1所成角的余弦值为
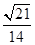 .
.(2)因点G在平面A1B1C1D1上,故可设G(x,y,2).
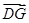 =(x,y,2),
=(x,y,2),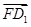 =(-2,-4,2),
=(-2,-4,2),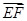 =(-1,1,0).由
=(-1,1,0).由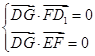
得
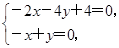 解得
解得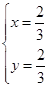
故当点G在面A1B1C1D1上,且到A1D1,C1D1距离均为
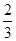 时,DG⊥D1EF
时,DG⊥D1EF
练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
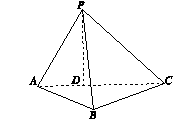
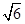 ,平面PAC⊥平面ABC,PD⊥AC于点D,AD=1,CD=3,PD=
,平面PAC⊥平面ABC,PD⊥AC于点D,AD=1,CD=3,PD=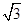 .
.
 的顶点
的顶点 分别在两两垂直的三条射线
分别在两两垂直的三条射线 上,则在下列命题中,错误的为( )
上,则在下列命题中,错误的为( )
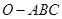 是正三棱锥
是正三棱锥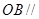 平面
平面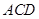
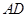 与
与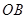 所成的角是
所成的角是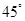
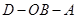 为
为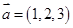 ,
,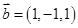 构成的向量集合
构成的向量集合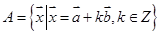 ,则向量
,则向量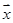 的模
的模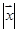 的最小值为 .
的最小值为 .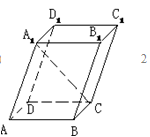

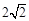
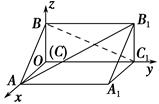



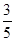
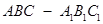 中,△
中,△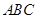 是边长为
是边长为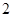 的等边三角形,
的等边三角形,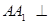 平面
平面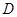 ,
,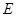 分别是
分别是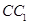 ,
,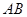 的中点.
的中点. 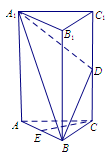
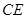 ∥平面
∥平面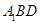 ;
;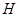 为
为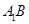 上的动点,当
上的动点,当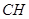 与平面
与平面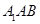 所成最大角的正切值为
所成最大角的正切值为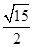 时,求平面
时,求平面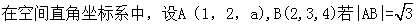 ,则实数a的值为( )
,则实数a的值为( )