题目内容
已知p:x2-8x-20≤0,q:x2-2x+1-m2≤0(m>0),若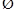 p是
p是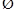 q的必要不充分条件,求实数m的取值范围.
q的必要不充分条件,求实数m的取值范围.
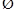 p是
p是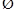 q的必要不充分条件,求实数m的取值范围.
q的必要不充分条件,求实数m的取值范围.m≥9
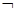 p:x2-8x-20>0,得x<-2或x>10,
p:x2-8x-20>0,得x<-2或x>10,设A={x|x<-2或x>10},
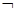 q:x2-2x+1-m2>0,得x<1-m,或x>1+m,
q:x2-2x+1-m2>0,得x<1-m,或x>1+m,设B={x|x<1-m或x>1+m}.
∵
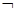 p是
p是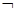 q的必要非充分条件,
q的必要非充分条件,∴B真包含于A,即
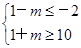
 m≥9.
m≥9.∴实数m的取值范围为m≥9.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
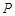 :
: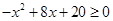 ,
,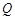 :
: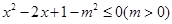 .
.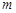 的取值范围;
的取值范围;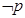 是
是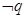 的必要不充分条件,求实数a的取值范围.
的必要不充分条件,求实数a的取值范围.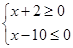 命题q:1-m≤x≤1+m,m>0,若¬p是¬q的必要不充分
命题q:1-m≤x≤1+m,m>0,若¬p是¬q的必要不充分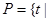 数列
数列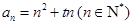 单调递增
单调递增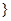 ,集合
,集合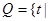 函数
函数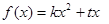 在区间
在区间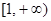 上单调递增
上单调递增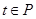 ”是“
”是“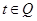 ”的充分不必要条件,则实数
”的充分不必要条件,则实数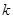 的最小值为 .
的最小值为 .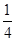 ≤
≤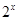 ≤
≤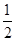 ,命题q:x+
,命题q:x+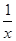 ∈
∈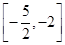 ,则下列说法正确的是 ( ).
,则下列说法正确的是 ( ). α.条件甲:m⊥a,m⊥b;条件乙:m⊥α,则“条件乙成立”是“条件甲成立”的( )
α.条件甲:m⊥a,m⊥b;条件乙:m⊥α,则“条件乙成立”是“条件甲成立”的( )