题目内容
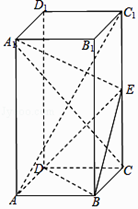
【题目】如图所示，在正方体ABCD﹣A1B1C1D1中，M，E，F，N分别为A1B1 ， B1C1 ， C1D1 ， D1A1的中点，求证：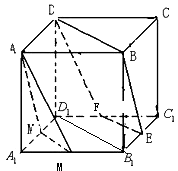 
（1）E，F，D，B四点共面；
（2）面AMN∥平面EFDB．
【答案】
（1）证明：∵E，E分别是B1C1，C1D1的中点，
∴EF∥B1D1，
∵B1D1∥BD，∴EF∥BD，
∴E，F，B，D，四点共面．
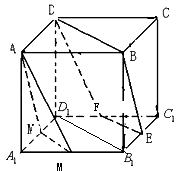
（2）证明：∵M，N分别是A1B1，D1A1的中点，
∴MN∥B1D1，
∵EF∥B1D1，∴MN∥EF，
∵F，N分别是D1C1、A1B1的中点，
∴NF 
A1D1，
∵ 
，∴NF AC，
∴四边形NFCA是平行四边形，
∴AN∥CF，
∵MN∩AN=N，EF∩DF=F，
∴面MAN∥面EFDB．
【解析】（1）由E，E分别是B1C1 ， C1D的中点，知EF∥B1D1 ， 从而得到EF∥BD，由此能证明E，F，B，D，四点共面．（2）由题设条件推导出MN∥EF，AN∥CF，由此能够证明面MAN∥面EFDB．
【考点精析】本题主要考查了平面的基本性质及推论和直线与平面平行的性质的相关知识点，需要掌握如果一条直线上的两点在一个平面内，那么这条直线在此平面内;过不在一条直线上的三点，有且只有一个平面;如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线；一条直线与一个平面平行，则过这条直线的任一平面与此平面的交线与该直线平行;简记为：线面平行则线线平行才能正确解答此题．
练习册系列答案
阅读快车系列答案
相关题目
