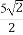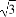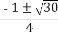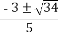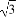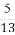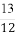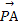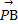Question

某人在C点测得某塔在南偏西80°,塔顶仰角为45°,此人沿南偏东40°方向前进10米到D,测得塔顶A的仰角为30°,则塔高为(　　)

(A)15米 (B)5米

(C)10米 (D)12米

 

Answer 1

C

【解析】【思路点拨】作出图形确定三角形,找到要用的角度和边长,利用余弦定理求得.

解:如图,设塔高为h米,在Rt△AOC中,∠ACO=45°,则OC=OA=h.

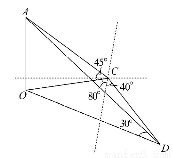
在Rt△AOD中,∠ADO=30°,则OD=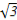h,

在△OCD中,∠OCD=120°,CD=10,

由余弦定理得:

OD2=OC2+CD2-2OC·CD·cos∠OCD,

即(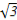h)2=h2+102-2h×10×cos 120°,

∴h2-5h-50=0,解得h=10或h=-5(舍去).

【方法技巧】测量高度的常见思路

解决高度的问题主要是根据条件确定出所利用的三角形,准确地理解仰角和俯角的概念并和三角形中的角度相对应;分清已知和待求的关系,正确地选择定理和公式,特别注意高度垂直地面构成的直角三角形.