题目内容
关于数列有下列四个判断:
①若 成等比数列,则
成等比数列,则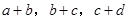 也成等比数列;②若数列{
也成等比数列;②若数列{ }既是等差数列也是等比数列,则{
}既是等差数列也是等比数列,则{ }为常数列;③数列{
}为常数列;③数列{ }的前n项和为
}的前n项和为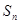 ,且
,且 ,则{
,则{ }为等差或等比数列;④数列{
}为等差或等比数列;④数列{ }为等差数列,且公差不为零,则数列{
}为等差数列,且公差不为零,则数列{ }中不会有
}中不会有 ,其中正确判断的序号是______.(注:把你认为正确判断的序号都填上)
,其中正确判断的序号是______.(注:把你认为正确判断的序号都填上)
②④
解析试题分析:①对于数列-1,1,-1,1,满足a,b,c,d成等比数列,但a+b=0,b+c=0,c+d=0,所以a+b,b+c,c+d不是等比数列,所以①错误.②若数列{an}既是等差数列又是等比数列,则数列{an}必是非零的常数列,所以an=an+1成立,所以②正确.③当a=0时,数列{an}既不是等差数列也不是等比数列,所以③错误.④在等差数列中,若am=an,则a1+(m-1)d=a1+(n-1)d,因为d≠0,所以m=n,与m≠n矛盾,所以④正确.故答案为:②④.
考点:命题的真假判断与应用;等差数列与等比数列的综合.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
 中,前
中,前 项和
项和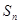 ,若
,若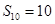 ,
,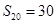 ,则
,则 = .
= .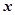 是4和16的等差中项,则
是4和16的等差中项,则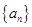 是公差不为零的等差数列,
是公差不为零的等差数列,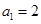 且
且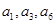 成等比数列,则
成等比数列,则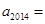 .
. 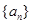 的前
的前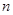 项和为
项和为 ,已知
,已知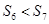 ,且
,且 ,则下列结论中正确的有 .(填序号)
,则下列结论中正确的有 .(填序号) ;
; ;
;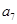 是数列
是数列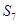 是数列
是数列 中的最小项.
中的最小项.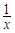 ,
,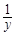 ,
, 成等差数列,则
成等差数列,则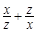 的值是 .
的值是 .