题目内容
函数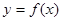 在一点的导数值为
在一点的导数值为 是函数
是函数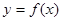 在这点取极值的( )
在这点取极值的( )
| A.充分条件 | B.必要条件 | C.必要非充分条件 | D.充要条件 |
C
解析试题分析:由极值的定义知,函数在某点处有极值,则此处导数必为零,若导数为0时,此点左右两边的导数符号可能相同,故不一定是极值,由此可以得出结论,极值点处导数比较0,导数为0处函数值不一定是极值.解:对于可导函数f(x)=x3,f'(x)=3x2,f'(0)=0,不能推出f(x)在x=0取极值,故导数为0时不一定取到极值,而对于任意的函数,当可导函数在某点处取到极值时,此点处的导数一定为0.故应选 C.
考点:函数取得极值的条件
点评:本题的考点是函数取得极值的条件,考查极值取到的条件,即对极值定义的正确理解.对概念的学习一定要掌握住其规范的逻辑结构,理顺其关系

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
函数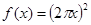 的导数是( )
的导数是( )
A.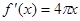 | B.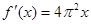 | C.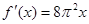 | D.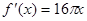 |
若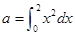 ,
, ,
,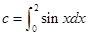 ,则
,则 、
、 、
、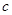 的大小关系是( )
的大小关系是( )
A.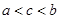 | B.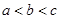 | C.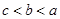 | D.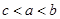 |
已知函数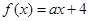 ,若
,若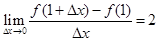 ,则实数
,则实数 的值为( )
的值为( )
A.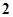 | B.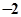 | C.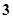 | D.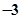 |
如图,函数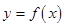 的图象在点P处的切线方程是
的图象在点P处的切线方程是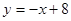 ,则
,则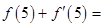 ( )
( )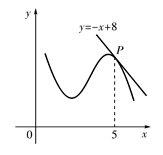
A.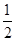 | B.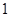 | C.2 | D.0 |
已知点 在曲线
在曲线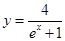 上,
上, 为曲线在点
为曲线在点 处的切线的倾斜角,则
处的切线的倾斜角,则 的取值范围为( )
的取值范围为( )
A.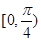 | B.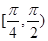 | C. | D.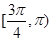 |
已知函数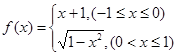 , 则
, 则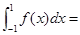 ( )
( )
A. | B.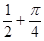 | C.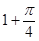 | D.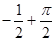 |
已知函数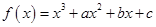 ,若
,若 在区间
在区间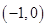 上单调递减,则
上单调递减,则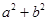 的取值范围是C
的取值范围是C
A.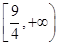 | B.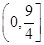 | C.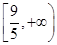 | D.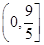 |
曲线f(x)=x㏑x在点x=1处的切线方程是( )
| A.y=2x+2 | B.y=2x-2 | C.y=x-1 | D.y=x+1 |