Question

【题目】已知椭圆和双曲线有共同焦点，是它们的一个交点，且，记椭圆和双曲线的离心率分别为，则的最大值为（ ）

A. 3B. 2C. D.

Answer 1

【答案】D

【解析】

设椭圆长半轴长为a1，双曲线的半实轴长a2，焦距2c．根据椭圆及双曲线的定义可以用a1，a2表示出|PF1|，|PF2|，在△F1PF2中根据余弦定理可得到，利用基本不等式可得结论．

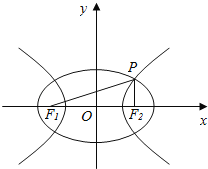
如图，设椭圆的长半轴长为a1，双曲线的半实轴长为a2，则根据椭圆及双曲线的定义：|PF1|+|PF2|＝2a1，|PF1|﹣|PF2|＝2a2，∴|PF1|＝a1+a2，|PF2|＝a1﹣a2，

设|F1F2|＝2c，∠F1PF2＝，则：在△PF1F2中，由余弦定理得，

4c2＝（a1+a2）2+（a1﹣a2）2﹣2（a1+a2）（a1﹣a2）cos

∴化简得：a12+3a22＝4c2，该式可变成：，

∴≥2

∴，

故选：D．