题目内容
已知f(A,B)=sin22A+cos22B-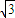 sin2A-cos2B+2.
sin2A-cos2B+2.(1)设△ABC的三内角为A、B、C,求f(A,B)取得最小值时,C的值;
(2)当A+B=
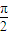 且A、B∈R时,y=f(A,B)的图象按向量
且A、B∈R时,y=f(A,B)的图象按向量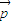 平移后得到函数y=2cos2A的图象,求满足上述条件的一个向量p.
平移后得到函数y=2cos2A的图象,求满足上述条件的一个向量p.
【答案】分析:(1)先对f(A,B)进行配方,然后可确定当sin2A-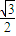 =0、cos2B-
=0、cos2B- =0时f(A,B)取最小值,进而根据正弦函数的性质可得到A、B、C的值.
=0时f(A,B)取最小值,进而根据正弦函数的性质可得到A、B、C的值.
(2)因为A+B=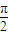 可得到2B=π-2A,然后将f(A,B)中的B用A替换得到关于A的函数,再由三角函数按向量平移的原则可得到向量
可得到2B=π-2A,然后将f(A,B)中的B用A替换得到关于A的函数,再由三角函数按向量平移的原则可得到向量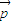 的坐标.
的坐标.
解答:解:(1)f(A,B)=(sin2A-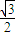 )2+(cos2B-
)2+(cos2B- )2+1,
)2+1,
由题意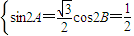 得
得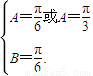
∴C=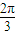 或C=
或C= .
.
(2)∵A+B=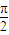 ,∴2B=π-2A,cos2B=-cos2A.
,∴2B=π-2A,cos2B=-cos2A.
∴f(A,B)=cos2A-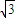 sin2A+3=2cos(2A+
sin2A+3=2cos(2A+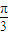 )+3=2cos2(A+
)+3=2cos2(A+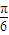 )+3.
)+3.
从而向量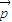 =(
=(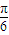 ,-3)(只要写出一个符合条件的向量p即可).
,-3)(只要写出一个符合条件的向量p即可).
点评:本题主要考查三角函数的基本性质和诱导公式的应用.三角函数部分公式比较多,要强化记忆.
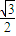 =0、cos2B-
=0、cos2B- =0时f(A,B)取最小值,进而根据正弦函数的性质可得到A、B、C的值.
=0时f(A,B)取最小值,进而根据正弦函数的性质可得到A、B、C的值.(2)因为A+B=
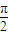 可得到2B=π-2A,然后将f(A,B)中的B用A替换得到关于A的函数,再由三角函数按向量平移的原则可得到向量
可得到2B=π-2A,然后将f(A,B)中的B用A替换得到关于A的函数,再由三角函数按向量平移的原则可得到向量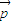 的坐标.
的坐标.解答:解:(1)f(A,B)=(sin2A-
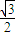 )2+(cos2B-
)2+(cos2B- )2+1,
)2+1,由题意
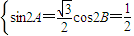 得
得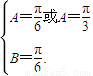
∴C=
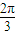 或C=
或C= .
.(2)∵A+B=
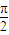 ,∴2B=π-2A,cos2B=-cos2A.
,∴2B=π-2A,cos2B=-cos2A.∴f(A,B)=cos2A-
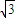 sin2A+3=2cos(2A+
sin2A+3=2cos(2A+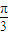 )+3=2cos2(A+
)+3=2cos2(A+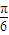 )+3.
)+3.从而向量
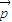 =(
=(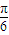 ,-3)(只要写出一个符合条件的向量p即可).
,-3)(只要写出一个符合条件的向量p即可).点评:本题主要考查三角函数的基本性质和诱导公式的应用.三角函数部分公式比较多,要强化记忆.

练习册系列答案
相关题目