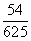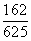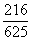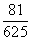题目内容
在一个口袋中装有12个大小相同的黑球、白球和红球。已知从袋中任意摸出2个球,至少得到一个黑球的概率是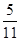 。
。
求:(1)袋中黑球的个数;
(2)从袋中任意摸出3个球,至少得到2个黑球的概率。
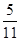 。
。求:(1)袋中黑球的个数;
(2)从袋中任意摸出3个球,至少得到2个黑球的概率。
(1)3(2)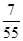
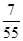
试题分析:(1)记“从袋中任意摸出2个球,至少得到1个黑球”为事件A,
设袋中黑球的个数为x,
则P(A)=1-P(
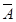 )=1-
)=1-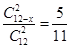 ,解得x=3或者x=20(舍去)
,解得x=3或者x=20(舍去)故黑球为3个
(2)记“从袋中任意摸出3个球,至少得到2个黑球”为事件B
则P(B)=
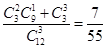
点评:古典概型概率的求解首先找到所有基本事件种数与满足题意要求的基本事件种数,然后求其比值

练习册系列答案
相关题目
 关于
关于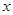 的线性回归方程
的线性回归方程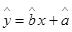 ,
,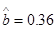
 ,
, ,若向区域
,若向区域 上随机投一点
上随机投一点 ,则点
,则点 的概率为____________。
的概率为____________。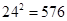 )
)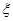 和
和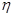 ,其中
,其中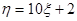 ,且
,且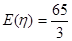 ,若
,若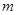 的值为
的值为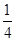
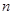
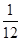
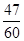 B.
B.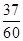 C.
C.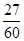 D.
D.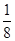
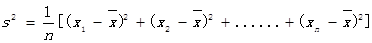 ,其中
,其中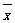 为x1,x2, ,xn的平均数)
为x1,x2, ,xn的平均数)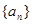 ,使得
,使得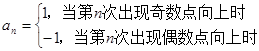 。记
。记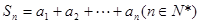 ,则
,则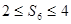 的概率为
的概率为 。(用数字作答)
。(用数字作答)