题目内容
设等差数列{an}的前项n和为Sn,且a5+a13=34,S3=9,
(Ⅰ)求数列{an}的通项公式及前n项和公式;
(Ⅱ)设数列{bn}的通项公式为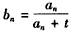 ,问:是否存在正整数t,使得b1,b2,bm(m≥3,m∈N)成等差数列?若存在,求出t和m的值;若不存在,请说明理由。
,问:是否存在正整数t,使得b1,b2,bm(m≥3,m∈N)成等差数列?若存在,求出t和m的值;若不存在,请说明理由。
(Ⅰ)求数列{an}的通项公式及前n项和公式;
(Ⅱ)设数列{bn}的通项公式为
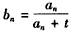 ,问:是否存在正整数t,使得b1,b2,bm(m≥3,m∈N)成等差数列?若存在,求出t和m的值;若不存在,请说明理由。
,问:是否存在正整数t,使得b1,b2,bm(m≥3,m∈N)成等差数列?若存在,求出t和m的值;若不存在,请说明理由。 解:(Ⅰ)设等差数列{an}的公差为d,
由已知得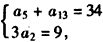 ,即
,即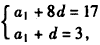 ,解得
,解得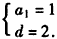 ,
,
故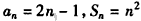 。
。
(Ⅱ)由(Ⅰ)知,要使b1,b2,bm成等差数列,必须 ,
,
即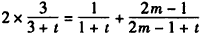 ,
,
整理,得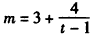 ,
,
因为m,t为正整数,所以t只能取2,3,5,
当t=2时,m=7;当t=3时,m=5;当t=5时,m=4。
故存在正整数t,使得b1,b2,bm成等差数列。
由已知得
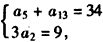 ,即
,即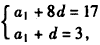 ,解得
,解得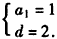 ,
,故
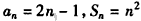 。
。(Ⅱ)由(Ⅰ)知,要使b1,b2,bm成等差数列,必须
 ,
,即
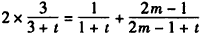 ,
,整理,得
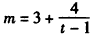 ,
,因为m,t为正整数,所以t只能取2,3,5,
当t=2时,m=7;当t=3时,m=5;当t=5时,m=4。
故存在正整数t,使得b1,b2,bm成等差数列。

练习册系列答案
相关题目