题目内容
在平面直角坐标系![]() O
O![]() 中,直线
中,直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() 、
、![]() 两点。
两点。
(Ⅰ)求证:“如果直线![]() 过点
过点![]() ,那么
,那么![]()
![]() =
=![]() ”是真命题;
”是真命题;
(Ⅱ)写出(Ⅰ)中命题的逆命题,判断它是真命题还是假命题,并说明理由。
(Ⅰ)证明见解析。
(Ⅱ)(Ⅰ)中命题的逆命题:在平面直角坐标系![]() O
O![]() 中,直线
中,直线![]() 与抛物线
与抛物线![]() =2
=2![]() 相交于
相交于![]() 、
、![]() 两点。如果
两点。如果![]()
![]() =
=![]() ,那么直线
,那么直线![]() 必过点
必过点![]() 。它是假命题,理由见解析。
。它是假命题,理由见解析。
解析:
(Ⅰ)证明:如果直线![]()
![]() 轴,则
轴,则![]() ;如果直线
;如果直线![]() 与
与![]() 轴不垂直,设直线
轴不垂直,设直线![]() 的方程为
的方程为![]() ,
,

![]()
![]()
![]()
![]() 。综上,“如果直线
。综上,“如果直线![]() 过点
过点![]() ,那么
,那么![]()
![]() =
=![]() ”是真命题。
”是真命题。
(Ⅱ)(Ⅰ)中命题的逆命题:在平面直角坐标系![]() O
O![]() 中,直线
中,直线![]() 与抛物线
与抛物线![]() =2
=2![]() 相交于
相交于![]() 、
、![]() 两点。如果
两点。如果![]()
![]() =
=![]() ,那么直线
,那么直线![]() 必过点
必过点![]() 。
。
设直线![]() 与
与![]() 轴的交点坐标为
轴的交点坐标为![]() ,则直线方程为
,则直线方程为![]() ,把它代入
,把它代入![]() 得
得
![]() 。
。
由![]() ,即直线
,即直线![]() 必过点
必过点![]() 。
。
∴(Ⅰ)中命题的逆命题是假命题。

练习册系列答案
相关题目
 O
O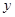 中,直线
中,直线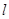 与抛物线
与抛物线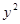 =2
=2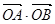 =3”是真命题;
=3”是真命题;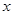 O
O 中,直线
中,直线 与抛物线
与抛物线 =2
=2 =3”是真命题;
=3”是真命题;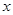 O
O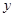 中,直线
中,直线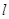 与抛物线
与抛物线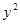 =2
=2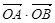 =3”是真命题;
=3”是真命题;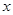 O
O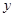 中,直线
中,直线 与抛物线
与抛物线 相交于
相交于 、
、 两点。
两点。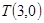 ,那么
,那么
 =
= ”是真命题;
”是真命题;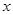 O
O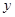 中,直线
中,直线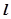 与抛物线
与抛物线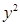 =2
=2 过点T(3,0),那么
过点T(3,0),那么
 =3”是真命题;
=3”是真命题;