题目内容
在平面直角坐标系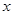 O
O 中,直线
中,直线 与抛物线
与抛物线 =2
=2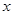 相交于A、B两点。
相交于A、B两点。
(1)求证:命题“如果直线 过点T(3,0),那么
过点T(3,0),那么 =3”是真命题;
=3”是真命题;
(2)写出(1)中命题的逆命题,判断它是真命题还是假命题,并说明理由。
(1)设过点T(3,0)的直线l交抛物线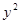 =2x于点A(x1,y1)、B(x2,y2). 当直线l的斜率不存在时A(3,
=2x于点A(x1,y1)、B(x2,y2). 当直线l的斜率不存在时A(3,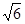 )、B(3,-
)、B(3,-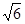 ),∴
),∴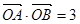 当直线l的斜率存在时,设直线l的方程为y=k(x-3),其中k≠0.
当直线l的斜率存在时,设直线l的方程为y=k(x-3),其中k≠0.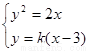 得ky2-2y-6k=0,则y1y2=-6. 又∵x1=
得ky2-2y-6k=0,则y1y2=-6. 又∵x1=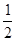 y12, x2=
y12, x2=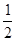 y22,
y22,
∴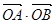 =x1x2+y1y2=
=x1x2+y1y2=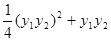 ="3." 综上所述, 命题是真命题.
="3." 综上所述, 命题是真命题.
(2)逆命题是:“设直线l交抛物线y2=2x于A、B两点,如果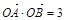 ,那么该直线过点T(3,0).”,假命题
,那么该直线过点T(3,0).”,假命题
【解析】
试题分析:(1)设过点T(3,0)的直线l交抛物线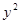 =2x于点A(x1,y1)、B(x2,y2).
=2x于点A(x1,y1)、B(x2,y2).
当直线l的斜率不存在时,直线l的方程为x=3,此时,直线l与抛物线相交于A(3,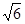 )、B(3,-
)、B(3,-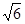 ),∴
),∴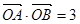
当直线l的斜率存在时,设直线l的方程为y=k(x-3),其中k≠0.
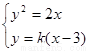 得ky2-2y-6k=0,则y1y2=-6. 又∵x1=
得ky2-2y-6k=0,则y1y2=-6. 又∵x1=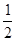 y12, x2=
y12, x2=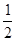 y22,
y22,
∴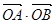 =x1x2+y1y2=
=x1x2+y1y2=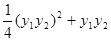 =3.
=3.
综上所述, 命题“......”是真命题.
(2)逆命题是:“设直线l交抛物线y2=2x于A、B两点,如果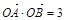 ,那么该直线过点T(3,0).”…10分,该命题是假命题. 例如:取抛物线上的点A(2,2),B(
,那么该直线过点T(3,0).”…10分,该命题是假命题. 例如:取抛物线上的点A(2,2),B(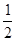 ,1),此时
,1),此时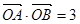 =3,直线AB的方程为y =
=3,直线AB的方程为y =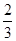 (x+1),而T(3,0)不在直线AB上.
(x+1),而T(3,0)不在直线AB上.
考点:直线与抛物线相交问题及四种命题
点评:直线与圆锥曲线相交时,常联立方程组,整理为关于x的二次方程,利用韦达定理找到根与系数的关系,通过设而不求的方法转化所求问题;四种命题中原命题与逆否命题真假性一致,逆命题与否命题真假性一致

 黄冈创优卷系列答案
黄冈创优卷系列答案 O
O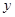 中,直线
中,直线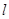 与抛物线
与抛物线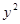 =2
=2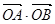 =3”是真命题;
=3”是真命题;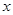 O
O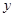 中,直线
中,直线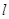 与抛物线
与抛物线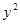 =2
=2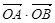 =3”是真命题;
=3”是真命题;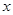 O
O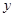 中,直线
中,直线 与抛物线
与抛物线 相交于
相交于 、
、 两点。
两点。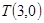 ,那么
,那么
 =
= ”是真命题;
”是真命题;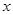 O
O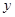 中,直线
中,直线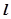 与抛物线
与抛物线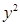 =2
=2 过点T(3,0),那么
过点T(3,0),那么
 =3”是真命题;
=3”是真命题;