题目内容
(本题12分)在平面直角坐标系 O
O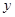 中,直线
中,直线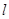 与抛物线
与抛物线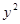 =2
=2 相交于A、B两点。
相交于A、B两点。
(1)求证:命题“如果直线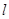 过点T(3,0),那么
过点T(3,0),那么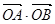 =3”是真命题;
=3”是真命题;
(2)写出(1)中命题的逆命题,判断它是真命题还是假命题,并说明理由。
1)利用坐标运算
(2)逆命题是:“设直线l交抛物线y2=2x于A、B两点,如果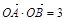 ,那么该直线过点T(3,0).”,该命题是假命题.
,那么该直线过点T(3,0).”,该命题是假命题.
【解析】
试题分析:1)解法一:设过点T(3,0)的直线l交抛物线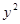 =2x于点A(x1,y1)、B(x2,y2).
=2x于点A(x1,y1)、B(x2,y2).
当直线l的斜率不存在时,直线l的方程为x=3,此时,直线l与抛物线相交于A(3,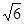 )、B(3,-
)、B(3,-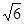 ),∴
),∴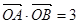 ……3分
……3分
当直线l的斜率存在时,设直线l的方程为y=k(x-3),其中k≠0.
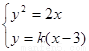 得ky2-2y-6k=0,则y1y2=-6. 又∵x1=
得ky2-2y-6k=0,则y1y2=-6. 又∵x1=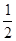 y12, x2=
y12, x2=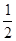 y22,
y22,
∴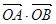 =x1x2+y1y2=
=x1x2+y1y2=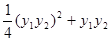 ="3."
="3."
综上所述, 命题“......”是真命题.
解法二:设直线l的方程为my =x-3与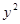 ="2x"
联立得到y2-2my-6=0
="2x"
联立得到y2-2my-6=0 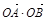 =x1x2+y1y2
=x1x2+y1y2
=(my1+3) (my2+3)+ y1y2=(m2+1) y1y2+3m(y1+y2)+9=(m2+1)× (-6)+3m×2m+9=3
(2)逆命题是:“设直线l交抛物线y2=2x于A、B两点,如果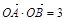 ,那么该直线过点T(3,0).”,该命题是假命题. 例如:取抛物线上的点A(2,2),B(
,那么该直线过点T(3,0).”,该命题是假命题. 例如:取抛物线上的点A(2,2),B(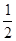 ,1),此时
,1),此时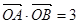 =3,直线AB的方程为y =
=3,直线AB的方程为y =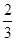 (x+1),而T(3,0)不在直线AB上.……12分
(x+1),而T(3,0)不在直线AB上.……12分
考点:本题主要考查抛物线的几何性质,直线好抛物线的位置关系,命题的概念及四种命题的关系,向量的坐标运算。
点评:本题以命题的真假探究为背景,重点考查直线与抛物线的位置关系,此类问题,往往通过联立方程组,应用韦达定理,实现整体代换,简化解题过程。

 与坐标轴的交点都在圆C上。
与坐标轴的交点都在圆C上。 截得的弦长为
截得的弦长为 ,求
,求 的值。
的值。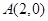 ,
,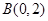 ,
,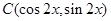 ,
,
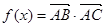 求
求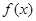 的表达式和最小正周期;
的表达式和最小正周期;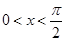 时,求
时,求