题目内容
在平面直角坐标系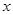 O
O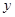 中,直线
中,直线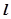 与抛物线
与抛物线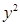 =2
=2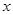 相交于A、B两点.
相交于A、B两点.
(1)求证:“如果直线 过点T(3,0),那么
过点T(3,0),那么
 =3”是真命题;
=3”是真命题;
(2)写出(1)中命题的逆命题,判断它是真命题还是假命题,并说明理由.
【答案】
解:(1)设过点T(3,0)的直线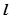 交抛物线y2=2x于点A(x1,y1)、B(x2,y2).
交抛物线y2=2x于点A(x1,y1)、B(x2,y2).
当直线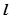 的钭率不存在时,直线
的钭率不存在时,直线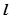 的方程为x=3,此
的方程为x=3,此
时,直线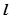 与抛物线相交于点A(3,
与抛物线相交于点A(3,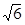 )、----------------------------------------------------(2分)
)、----------------------------------------------------(2分)
B(3,-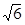 ). ∴
). ∴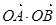 =3;
-----------------------------------------------------------(4分)
=3;
-----------------------------------------------------------(4分)
当直线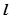 的钭率存在时,设直线
的钭率存在时,设直线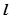 的方程为
的方程为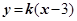 ,其中
,其中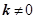 ,
,
由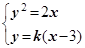 得
得 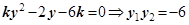 -----------------------(6分)
-----------------------(6分)
又 ∵ 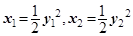 ,
,
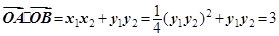 ,
,
综上所述,命题“如果直线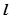 过点T(3,0),那么
过点T(3,0),那么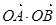 =3”是真命题;---------------(8分)
=3”是真命题;---------------(8分)
(2)逆命题是:设直线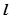 交抛物线y2=2x于A,
B两点,如果
交抛物线y2=2x于A,
B两点,如果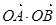 =3,那么该直线过点
=3,那么该直线过点
T(3,0) 。 .该命题是假命题.-------------------------------------------------------------(10分)
例如:取抛物线上的点A(2,2),B(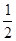 ,1),此时
,1),此时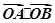 =3,直线AB的方程为:
=3,直线AB的方程为: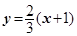 ,而T(3,0)不在直线AB上。-------------------------------------------
,而T(3,0)不在直线AB上。-------------------------------------------
【解析】略

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
 O
O 中,直线
中,直线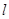 与抛物线
与抛物线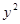 =2
=2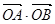 =3”是真命题;
=3”是真命题;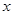 O
O 中,直线
中,直线 与抛物线
与抛物线 =2
=2 =3”是真命题;
=3”是真命题;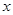 O
O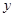 中,直线
中,直线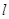 与抛物线
与抛物线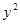 =2
=2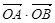 =3”是真命题;
=3”是真命题;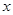 O
O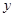 中,直线
中,直线 与抛物线
与抛物线 相交于
相交于 、
、 两点。
两点。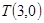 ,那么
,那么
 =
= ”是真命题;
”是真命题;