题目内容
在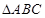 中,角
中,角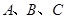 对边分别是
对边分别是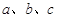 ,且满足
,且满足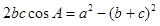 .
.
(Ⅰ)求角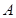 的大小;
的大小;
(Ⅱ)若 ,
,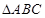 的面积为
的面积为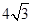 ;求
;求 .
.
(Ⅰ)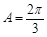 ;(Ⅱ)
;(Ⅱ)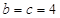 .
.
解析试题分析:(Ⅰ)利用余弦定理 得
得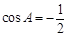 ,则
,则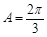 .(Ⅱ)利用三角形面积公式
.(Ⅱ)利用三角形面积公式 ,得出
,得出 ,而余弦定理
,而余弦定理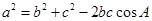 ,得出
,得出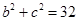 ,由上两式得出
,由上两式得出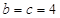 .
.
试题解析:(Ⅰ)由余弦定理得 ,代入
,代入 得
得 ,∴
,∴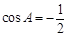 , ∵
, ∵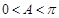 ,∴
,∴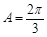
(Ⅱ) ,
,
解得: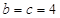 .
.
考点:1.向量数量积;2.余弦定理与三角形面积公式.

练习册系列答案
相关题目
题目内容
在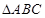 中,角
中,角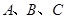 对边分别是
对边分别是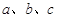 ,且满足
,且满足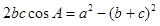 .
.
(Ⅰ)求角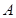 的大小;
的大小;
(Ⅱ)若 ,
,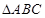 的面积为
的面积为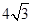 ;求
;求 .
.
(Ⅰ)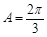 ;(Ⅱ)
;(Ⅱ)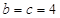 .
.
解析试题分析:(Ⅰ)利用余弦定理 得
得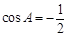 ,则
,则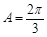 .(Ⅱ)利用三角形面积公式
.(Ⅱ)利用三角形面积公式 ,得出
,得出 ,而余弦定理
,而余弦定理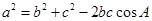 ,得出
,得出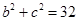 ,由上两式得出
,由上两式得出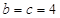 .
.
试题解析:(Ⅰ)由余弦定理得 ,代入
,代入 得
得 ,∴
,∴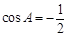 , ∵
, ∵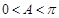 ,∴
,∴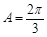
(Ⅱ) ,
,
解得: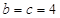 .
.
考点:1.向量数量积;2.余弦定理与三角形面积公式.
