题目内容
已知函数f(x)=cos 2x+2sin x·sin.
(1)求f(x)的最小正周期,最大值以及取得最大值时x的集合;
(2)若A是锐角三角形△ABC的内角,f(A)=0,b=5,a=7,求△ABC的面积.
(1)π,2,;(2)10.
解析试题分析:(1)将函数f(x)展开,由倍角公式及诱导公式化简为f(x)=2sin,即可得f(x)的最小正周期,最大值.令2x+=+2kπ,k∈Z,可得取得最大值时x的集合为;
(2)先由f(A)=sin=0及锐角A的范围得A=,再由b=5,a=7根据余弦定理得c=8,最后由三角形面积公式S△ABC=bc·sin A得到△ABC的面积为10.
试题解析:(1)f(x)=cos 2x+2sin x·sin=cos 2x+2sin x·cos x
=cos 2x+sin 2x=2sin, 3分
∴f(x)的最小正周期是π. 4分
令2x+=+2kπ,k∈Z.解得:x=+kπ,k∈Z.
∴f(x)的最大值是2,取得最大值时x的集合是. 6分
(2)∵f(A)=sin=0,0<A<,∴A=, 8分
在△ABC中,a2=b2+c2-2bc·cos A,c2-5c-24=0,解得c=8或c=-3(舍), 10分
∴S△ABC=bc·sin A=10. 12分
考点:1.三角恒等变换;2.余弦定理;3.三角形面积公式

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
 两个小岛相距10
两个小岛相距10 ,船O将保持观望A岛和B岛所成的视角为
,船O将保持观望A岛和B岛所成的视角为 ,现从船O上派下一只小艇沿
,现从船O上派下一只小艇沿 方向驶至
方向驶至 处进行作业,且
处进行作业,且 .设
.设

 分别表示
分别表示 和
和 ,并求出
,并求出 的距离为
的距离为 ,求BD的最大值.
,求BD的最大值.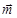 =(sinA,1),
=(sinA,1),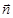 =(cosA,
=(cosA,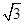 ),且
),且 ,求△ABC的面积.
,求△ABC的面积. 处下山至
处下山至 处有两条路径.一条是从
处有两条路径.一条是从 ,然后从
,然后从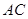 匀速步行,速度为
匀速步行,速度为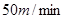 .在甲出发
.在甲出发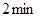 后,乙从
后,乙从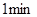 后,再从
后,再从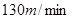 ,索道
,索道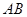 长为
长为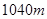 ,经测量
,经测量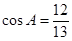 ,
,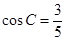 .
.
 分钟,乙步行的速度应控制在什么范围内?
分钟,乙步行的速度应控制在什么范围内?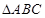 中,角
中,角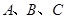 对边分别是
对边分别是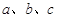 ,且满足
,且满足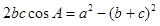 .
.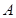 的大小;
的大小; ,
,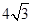 ;求
;求 .
. 的外接圆半径
的外接圆半径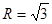 ,角
,角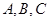 的对边分别是
的对边分别是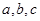 ,且
,且 .
.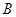 和边长
和边长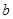 ;
;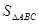 的最大值及取得最大值时的
的最大值及取得最大值时的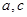 的值,并判断此时三角形的形状.
的值,并判断此时三角形的形状. 中,内角
中,内角 所对的边长分别为
所对的边长分别为 ,
,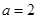 ,
,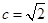 ,
,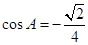 .
. 是锐角三角形,
是锐角三角形, 分别是内角A,B,C所对边长,并且
分别是内角A,B,C所对边长,并且
 ,求
,求 (其中
(其中 ).
).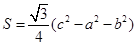 .
.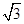 ,求A.
,求A.