题目内容
(本小题满分12分)某企业准备投产一批特殊型号的产品,已知该种产品的成本 与产量
与产量 的函数关系式为
的函数关系式为
该种产品的市场前景无法确定,有三种可能出现的情况,各种情形发生的概率及产品价格 与产量
与产量 的函数关系式如下表所示:
的函数关系式如下表所示:
设 分别表示市场情形好、中差时的利润,随机变量
分别表示市场情形好、中差时的利润,随机变量 ,表示当产量为
,表示当产量为 ,而市场前景无法确定的利润.
,而市场前景无法确定的利润.
(I)分别求利润 与产量
与产量 的函数关系式;
的函数关系式;
(II)当产量 确定时,求期望
确定时,求期望 ;
;
(III)试问产量 取何值时,
取何值时, 取得最大值.
取得最大值.
 与产量
与产量 的函数关系式为
的函数关系式为
该种产品的市场前景无法确定,有三种可能出现的情况,各种情形发生的概率及产品价格
 与产量
与产量 的函数关系式如下表所示:
的函数关系式如下表所示:| 市场情形 | 概率 | 价格 与产量 与产量 的函数关系式 的函数关系式 |
| 好 | 0.4 |  |
| 中 | 0.4 |  |
| 差 | 0.2 |  |
 分别表示市场情形好、中差时的利润,随机变量
分别表示市场情形好、中差时的利润,随机变量 ,表示当产量为
,表示当产量为 ,而市场前景无法确定的利润.
,而市场前景无法确定的利润.(I)分别求利润
 与产量
与产量 的函数关系式;
的函数关系式;(II)当产量
 确定时,求期望
确定时,求期望 ;
;(III)试问产量
 取何值时,
取何值时, 取得最大值.
取得最大值.(I)L1=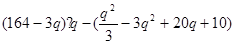
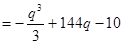 (q>0).
(q>0).
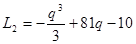 (q>0)
(q>0)
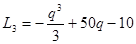 (q>0)
(q>0)
(II)
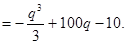
(III)当q=10时, f(q)取得最大值,即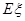 最大时的产量q为10.
最大时的产量q为10.
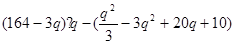
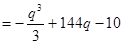 (q>0).
(q>0).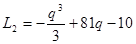 (q>0)
(q>0)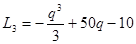 (q>0)
(q>0)(II)

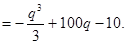
(III)当q=10时, f(q)取得最大值,即
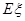 最大时的产量q为10.
最大时的产量q为10.解:由题意可得
L1=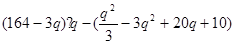
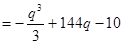 (q>0).
(q>0).
同理可得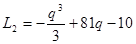 (q>0)
(q>0)
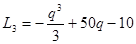 (q>0) 4分
(q>0) 4分
(Ⅱ) 解:由期望定义可知
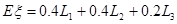
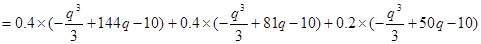
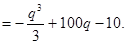
(Ⅲ) 解:由(Ⅱ)可知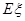 是产量q的函数,设
是产量q的函数,设
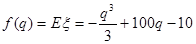 (q>0)
(q>0)
得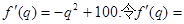 0解得
0解得
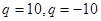 (舍去).
(舍去).
由题意及问题的实际意义(或当0<q<10时,f′(q)>0;当q>10时, f(q) <0=可知,当q=10时, f(q)取得最大值,即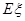 最大时的产量q为10.
最大时的产量q为10.
L1=
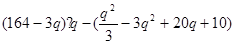
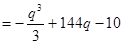 (q>0).
(q>0).同理可得
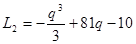 (q>0)
(q>0)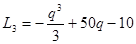 (q>0) 4分
(q>0) 4分(Ⅱ) 解:由期望定义可知
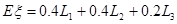
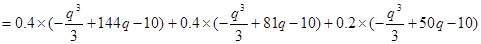
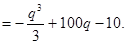
(Ⅲ) 解:由(Ⅱ)可知
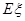 是产量q的函数,设
是产量q的函数,设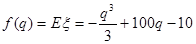 (q>0)
(q>0)得
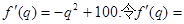 0解得
0解得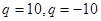 (舍去).
(舍去).由题意及问题的实际意义(或当0<q<10时,f′(q)>0;当q>10时, f(q) <0=可知,当q=10时, f(q)取得最大值,即
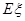 最大时的产量q为10.
最大时的产量q为10.
练习册系列答案
相关题目
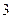 次;在
次;在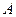 处每投进一球得
处每投进一球得 处每投进一球得
处每投进一球得 分;如果前两次得分之和超过
分;如果前两次得分之和超过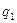 为
为 ,在
,在 ,该同学选择先在
,该同学选择先在 表示该同学投篮训练结束后所得的总分,其分布列为
表示该同学投篮训练结束后所得的总分,其分布列为
 (简称血酒含量,单位是毫克/100毫升),当
(简称血酒含量,单位是毫克/100毫升),当 时,为酒后驾车;当
时,为酒后驾车;当 时,为醉酒驾车淮安市公安局交通管理部门于2010年6月的一天对某路段的一次拦查行动中,依法检查了200辆机动车驾驶员的血酒含量,其中查处酒后驾车的有6人,查处醉酒驾车的有4人,依据上述材料回答下列问题:
时,为醉酒驾车淮安市公安局交通管理部门于2010年6月的一天对某路段的一次拦查行动中,依法检查了200辆机动车驾驶员的血酒含量,其中查处酒后驾车的有6人,查处醉酒驾车的有4人,依据上述材料回答下列问题: 的分布列和期望;
的分布列和期望; ,甲、乙都闯关成功的概率为
,甲、乙都闯关成功的概率为 ,乙、丙都闯关成功的概率为
,乙、丙都闯关成功的概率为 ,每人闯关成功得2分,三人得分之和记为小组团体总分.
,每人闯关成功得2分,三人得分之和记为小组团体总分. 与
与 轴所围成阴影部分的概率为 .
轴所围成阴影部分的概率为 . 
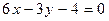 ,向边长为2的正方形内随机地投飞镖,飞镖都能投入正方形内,且投到每个点的可能性相等,
,向边长为2的正方形内随机地投飞镖,飞镖都能投入正方形内,且投到每个点的可能性相等,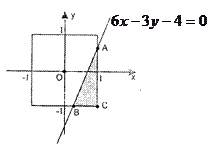
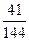
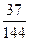
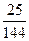
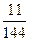
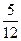
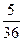
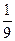
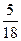

 ,分别写在6张小卡片上,放入盒中.
,分别写在6张小卡片上,放入盒中. 的分布列和数学期望.
的分布列和数学期望.