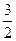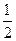题目内容
如图所示,抛物线y=4-x2与直线y=3x的两交点为A、B,点P在抛物线上从A向B运动.

(1)求使△PAB的面积最大的P点的坐标(a,b);
(2)证明由抛物线与线段AB围成的图形,被直线x=a分为面积相等的两部分.

(1)求使△PAB的面积最大的P点的坐标(a,b);
(2)证明由抛物线与线段AB围成的图形,被直线x=a分为面积相等的两部分.
(1)P点的坐标为(-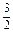 ,
,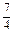 )时,△PAB的面积最大(2)证明见解析
)时,△PAB的面积最大(2)证明见解析
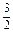 ,
,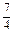 )时,△PAB的面积最大(2)证明见解析
)时,△PAB的面积最大(2)证明见解析(1) 解方程组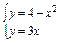 ,得x1=1,x2=-4.
,得x1=1,x2=-4.
∴抛物线y=4-x2与直线y=3x的交点为
A(1,3),B(-4,-12),
∴P点的横坐标a∈(-4,1).
点P(a,b)到直线y=3x的距离为d=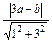 ,
,
∵P点在抛物线上,∴b=4-a2,
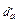 =
=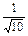 ·(4-3a-a2)′=
·(4-3a-a2)′=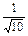 (-2a-3)=0,
(-2a-3)=0,
∴a=-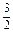 ,即当a=-
,即当a=-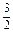 时,d最大,
时,d最大,
这时b=4-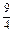 =
=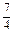 ,
,
∴P点的坐标为(-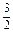 ,
,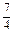 )时,△PAB的面积最大.
)时,△PAB的面积最大.
(2) 设上述抛物线与直线所围成图形的面积为S,
位于x=-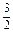 右侧的面积为S1.
右侧的面积为S1.
S=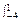 (4-x2-3x)dx=
(4-x2-3x)dx=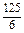 ,
,
S1=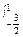 (4-x2-3x)dx=
(4-x2-3x)dx=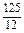 ,
,
∴S=2S1,即直线x=-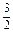 平分抛物线与线段AB围成的图形的面积.
平分抛物线与线段AB围成的图形的面积.
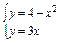 ,得x1=1,x2=-4.
,得x1=1,x2=-4.∴抛物线y=4-x2与直线y=3x的交点为
A(1,3),B(-4,-12),
∴P点的横坐标a∈(-4,1).
点P(a,b)到直线y=3x的距离为d=
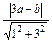 ,
,∵P点在抛物线上,∴b=4-a2,
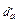 =
=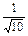 ·(4-3a-a2)′=
·(4-3a-a2)′=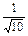 (-2a-3)=0,
(-2a-3)=0,∴a=-
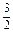 ,即当a=-
,即当a=-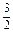 时,d最大,
时,d最大,这时b=4-
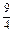 =
=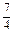 ,
,∴P点的坐标为(-
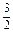 ,
,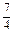 )时,△PAB的面积最大.
)时,△PAB的面积最大.(2) 设上述抛物线与直线所围成图形的面积为S,
位于x=-
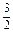 右侧的面积为S1.
右侧的面积为S1.S=
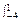 (4-x2-3x)dx=
(4-x2-3x)dx=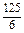 ,
,S1=
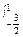 (4-x2-3x)dx=
(4-x2-3x)dx=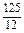 ,
,∴S=2S1,即直线x=-
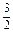 平分抛物线与线段AB围成的图形的面积.
平分抛物线与线段AB围成的图形的面积.
练习册系列答案
相关题目
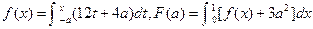 求函数
求函数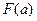 的最小值.
的最小值.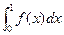 =5,
=5,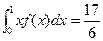 ,那么f(x)的解析式是______.
,那么f(x)的解析式是______. 过点
过点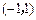 ,
,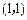 .
.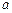 表示曲线与
表示曲线与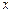 轴所围成的图形面积
轴所围成的图形面积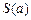 ;
; (|x-1|+|x-3|)dx.
(|x-1|+|x-3|)dx.
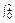 x(x+1)dx;
x(x+1)dx; (e2x+
(e2x+ )dx;
)dx; sin2xdx.
sin2xdx.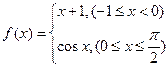 的图象与x轴所围成的封闭图形的面积为( )
的图象与x轴所围成的封闭图形的面积为( )