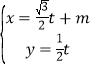题目内容
【题目】已知椭圆的中心在原点,焦点在x轴上,长轴的两个端点分别为![]() 、
、![]() .短轴的两个端点分别为
.短轴的两个端点分别为![]() ,
,![]() .菱形
.菱形![]() 的面积为
的面积为![]() ,离心率
,离心率![]() .
.
(1)求椭圆的标准方程;
(2)设![]() ,经过点M作斜率不为0的直线
,经过点M作斜率不为0的直线![]() 交椭圆C于A、B两点,若
交椭圆C于A、B两点,若![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]()
【解析】
(1)由已知条件得出关于![]() 方程组求解即可;
方程组求解即可;
(2)方法一:先由已知得出![]() 中垂线过
中垂线过![]() 点,设出直线
点,设出直线![]() 的方程,
的方程,![]() 点坐标,联立直线方程和椭圆方程,消去
点坐标,联立直线方程和椭圆方程,消去![]() 得关于
得关于![]() 的一元二次方程,利用韦达定理得出
的一元二次方程,利用韦达定理得出![]() 点坐标关系,最后利用
点坐标关系,最后利用![]() 中点在中垂线上得到关系式求解即可.方法二:先设出直线
中点在中垂线上得到关系式求解即可.方法二:先设出直线![]() 的方程,
的方程,![]() 点坐标,由已知向量关系式化简为坐标关系,利用点差法得出
点坐标,由已知向量关系式化简为坐标关系,利用点差法得出![]() 点坐标关系,然后把直线
点坐标关系,然后把直线![]() 方程与椭圆方程联立得关于
方程与椭圆方程联立得关于![]() 的一元二次方程,利用韦达定理即可得到等量关系,求解即可.
的一元二次方程,利用韦达定理即可得到等量关系,求解即可.
解:(1)∵![]() ,∴
,∴![]() .
.
又因为菱形![]() 的面积为
的面积为![]() ,即有
,即有![]() ,即
,即![]() ,
,
所以![]() ,从而
,从而![]() ,
,
所以椭圆C的标准方程为![]() .
.
(2)由![]() ,知
,知![]() ,设
,设![]() ,由向量加法的意义,知
,由向量加法的意义,知![]() 是线段
是线段![]() 的中垂线,设直线
的中垂线,设直线![]() 的方程为
的方程为![]() ,经过N且与
,经过N且与![]() 垂直的直线为
垂直的直线为![]() .
.
设![]() ,由
,由![]() 消去
消去![]() ,得
,得![]() ,
,
于是有![]() .
.
关于A,B关于直线![]() 对称,故点
对称,故点![]() 必在此直线上,
必在此直线上,
所以![]() ,即
,即![]() ,所以
,所以![]() 或
或![]() ,
,
故所求的直线![]() 的方程为
的方程为![]() 或
或![]() ,即
,即![]() 或
或![]() .
.
解法二:设![]() ,因为
,因为![]() ,所以
,所以
![]() .
.
由题得![]() ,即
,即
![]() .①
.①
因为A、B在椭圆C上,所以![]() ,所以
,所以![]() .两式相减,得
.两式相减,得![]() ,② 因为
,② 因为![]() 的斜率不为0,所以
的斜率不为0,所以![]() ,将②代①,得
,将②代①,得![]() .③
.③
因直线![]() 经过
经过![]() ,设直线
,设直线![]() 的方程为
的方程为![]() ,
,
由![]() 消去
消去![]() ,得
,得![]() ,
,
于是有![]() ,代入③得
,代入③得![]() ,解得
,解得![]() ,或
,或![]() .
.
故所求直线![]() 的方程为
的方程为![]() 或
或![]() ,即
,即![]() .或
.或![]() .
.

【题目】已知某次考试之后,班主任从全班同学中随机抽取一个容量为8的样本,他们的数学、物理成绩(单位:分)对应如下表,对应散点图如图所示:
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
数学成绩 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
物理成绩 | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
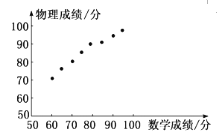
根据以上信息,则下列结论:
①根据散点图,可以判断数学成绩与物理成绩具有线性相关关系;
②根据散点图,可以判断数学成绩与物理成绩具有一次函数关系;
③从全班随机抽取2名同学(记为甲、乙),若甲同学的数学成绩为80分,乙同学的数学成绩为60分,则可以判断出甲同学的物理成绩一定比乙同学的物理成绩高;
④从全班随机抽取2名同学(记为甲、乙),若甲同学的数学成绩为80分,乙同学的数学成绩为60分,则不能判断出甲同学的物理成绩一定比乙同学的物理成绩高;
其中正确的个数是( )
A.1B.2C.3D.4