题目内容
已知二次函数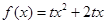

(Ⅰ)求不等式 的解集;
的解集;
(Ⅱ)若 ,记
,记 为数列
为数列 的前
的前 项和,且
项和,且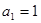 ,
,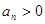
 ),点
),点 在函数
在函数 的图像上,求
的图像上,求 的表达式.
的表达式.
【答案】
(1)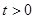 时, 解集是
时, 解集是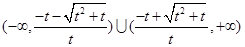 ;
;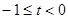 时,解集是
时,解集是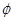 ;
; 时,解集是
时,解集是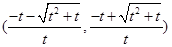
(2)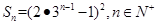
【解析】
试题分析:解:(Ⅰ)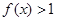 即:
即: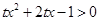 ,
,
①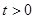 时,方程
时,方程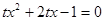 的判别式
的判别式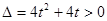 1分
1分
方程两根为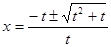 2分
2分
解集是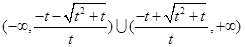 3分
3分
②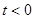 时,方程
时,方程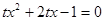 的判别式
的判别式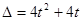
Ⅰ)当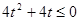 ,即
,即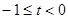 时,解集是
时,解集是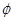 4分
4分
Ⅱ)当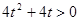 即
即 时,解集是
时,解集是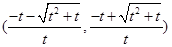 5分
5分
综上所述,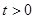 时, 解集是
时, 解集是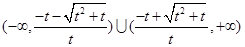 ;
;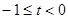 时,解集是
时,解集是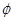 ;
; 时,解集是
时,解集是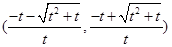 6分
6分
(Ⅱ)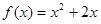 点
点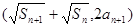 在函数
在函数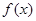 的图像上,
的图像上,
即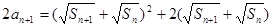 7分
7分
整理得
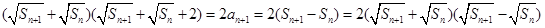
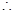
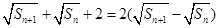
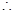
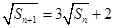 9分
9分
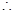
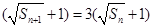 ,又
,又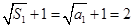 , 10分
, 10分
所以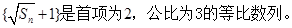
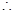
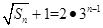
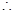
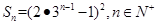 12分
12分
考点:等比数列
点评:主要是考查了等比数列的通项公式以及求和的运用,属于基础题。

练习册系列答案
相关题目
 (第三、四层次学校的学生做次题)
(第三、四层次学校的学生做次题)