题目内容
(2013•辽宁一模)在正三棱锥P-ABC中,有一半球,其底面与三棱锥的底面重合,正三棱锥的三个侧面都与半球相切,如果半球的半径等于1,则正三棱锥的体积最小时,正三棱锥的高等于( )
分析:画出图形,设三棱锥的高 PO=x,底面△ABC的AB边上的高 CD=y,求出x,y的关系,推出体积的表达式,利用函数的导数求出函数的最小值,即可求出高的值.
解答: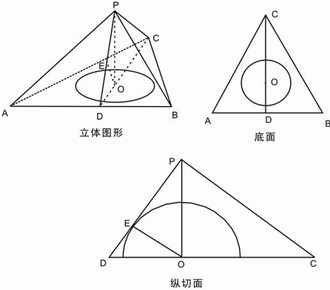 解:根据题意,画出图形如下,
解:根据题意,画出图形如下,
其中,立体图形只画出了半球的底面.
设三棱锥的高 PO=x,
底面△ABC的AB边上的高 CD=3•OD=3y
在纵切面图形可看出,Rt△PEO∽Rt△POD,
则
=
,而 PD=
,即
=
,整理得 x2y2=x2+y2,
所以 y2=
,
而三棱锥P-ABC的体积等于
×底面△ABC的面积×高PO,即V=
×
×AB×CD×PO=
×
×2
y×3y×x=
y2x=
,
对体积函数求导,得
V′=
,令V′=0,解得唯一正解 x=
,
由该体积函数的几何意义可知 x=
为其体积最小值点,
故三棱锥体积最小时Vmin=
,高为
.
故选D.
 解:根据题意,画出图形如下,
解:根据题意,画出图形如下,其中,立体图形只画出了半球的底面.
设三棱锥的高 PO=x,
底面△ABC的AB边上的高 CD=3•OD=3y
在纵切面图形可看出,Rt△PEO∽Rt△POD,
则
| PO |
| EO |
| PD |
| OD |
| PO2+OD2 |
| 1 |
| x |
| ||
| y |
所以 y2=
| x2 |
| x2-1 |
而三棱锥P-ABC的体积等于
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| ||
| x2-1 |
对体积函数求导,得
V′=
| ||
| (x2-1)2 |
| 3 |
由该体积函数的几何意义可知 x=
| 3 |
故三棱锥体积最小时Vmin=
| 9 |
| 2 |
| 3 |
故选D.
点评:本题考查几何体的内接球的问题,函数的导数的应用,考查空间想象能力以及计算能力.

练习册系列答案
相关题目