题目内容
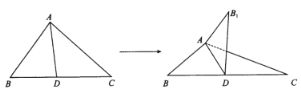
【题目】已知正△ABC边长为3,点M,N分别是AB,AC边上的点,AN=BM=1,如图1所示.将△AMN沿MN折起到△PMN的位置,使线段PC长为![]() ,连接PB,如图2所示.
,连接PB,如图2所示.
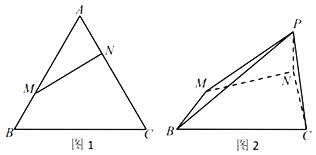
(Ⅰ)求证:平面PMN⊥平面BCNM;
(Ⅱ)若点D在线段BC上,且BD=2DC,求二面角M﹣PD﹣C的余弦值.
【答案】(Ⅰ)见解析(Ⅱ)![]() .
.
【解析】
(Ⅰ)推导出AN⊥MN,即PN⊥MN,PN⊥NC,从而PN⊥平面BCNM,由此能证明平面PMN⊥平面BCNM.
(Ⅱ)以N为坐标原点,NM为x轴,NC为y轴,NP为z轴,建立空间直角坐标系,利用向量法能求出二面角M﹣PD﹣C的余弦值.
解:(Ⅰ)证明:依题意,在△AMN中,AM=2,AN=1,∠A![]() ,
,
由余弦定理,![]() ,解得
,解得![]() ,
,
根据勾股定理得MN2+AN2=AM2,∴AN⊥MN,即PN⊥MN,
在图2△PNC中,PN=1,NC=2,PC![]() ,
,
∴PC2=PN2+NC2,∴PN⊥NC,
∵MN∩NC=N,∴PN⊥平面BCNM,
∵PN平面PMN,∴平面PMN⊥平面BCNM.
(Ⅱ)解:以N为坐标原点,NM为x轴,NC为y轴,NP为z轴,
建立空间直角坐标系,
则P(0,0,1),M(![]() ,0,0),D(
,0,0),D(![]() ,
,![]() ,0),C(0,2,0),
,0),C(0,2,0),
∴![]() (
(![]() ,0,﹣1),
,0,﹣1),![]() (
(![]() ,
,![]() ,0),
,0),
![]() (0,2,﹣1),
(0,2,﹣1),![]() (
(![]() ,
,![]() ,0),
,0),
设平面MPD的一个法向量![]() (x,y,z),
(x,y,z),
则 ,取y=1,得
,取y=1,得![]() (
(![]() ,1,3),
,1,3),
设平面PDC的法向量![]() (a,b,c),
(a,b,c),
则 ,取a=1,得
,取a=1,得![]() (1,
(1,![]() ,2
,2![]() ),
),
设二面角M﹣PD﹣C的平面角为θ,由图知θ是钝角,
∴cosθ .
.
二面角M﹣PD﹣C的余弦值为![]() .
.


练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目