题目内容
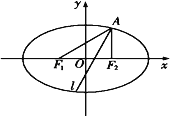
【题目】如图所示，已知椭圆E经过点
，对称轴为坐标轴，焦点
，
在x轴上，离心率e
．直线l是
的平分线，则椭圆E的方程是_____，l所在的直线方程是_____．
【答案】
．
【解析】
第一空：设出椭圆方程，根据椭圆E经过点
，离心率
，建立方程组，求得几何量，即可得到椭圆E的方程；
第二空：求得AF1方程、AF2方程，利用角平分线性质，即可求得∠F1AF2的平分线所在直线l的方程．
解：第一空：设椭圆方程为
，（a＞b＞0）
∵椭圆E经过点，离心率e
，
∴
e，
1，
∴a2＝16，b2＝12，
∴椭圆方程E为：；
第二空：由椭圆方程可得
，
，
∵，
∴AF1方程为：
，AF2方程为：x＝2，
设角平分线上任意一点为P（x，y），则
．
得或
，
∵斜率为正，
∴直线方程为；
故答案为：；．
练习册系列答案
快乐小博士巩固与提高系列答案
相关题目
