题目内容
1.已知函数f(x)=ex-x+$\frac{1}{2}$x2.(1)求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)设g(x)=ex+$\frac{1}{2}$x2-2lnx+a-1-f′(x),若g(x)≥0,求实数a的取值范围.
分析 (1)求出f(x)的导数,求得切线的斜率和切点,由点斜式方程,可得切线方程;
(2)化简g(x),运用参数分离,构造函数,求得导数和单调区间、极值也为最值,可得a的范围.
解答 解:(1)函数f(x)=ex-x+$\frac{1}{2}$x2的导数为f′(x)=ex-1+x,
曲线y=f(x)在点(1,f(1))处的切线斜率为k=f′(1)=e,
切点为(1,e-$\frac{1}{2}$),
即有曲线y=f(x)在点(1,f(1))处的切线方程为y-(e-$\frac{1}{2}$)=e(x-1),
即为ex-y-$\frac{1}{2}$=0;
(2)由于f′(x)=ex-1+x,
则g(x)=ex+$\frac{1}{2}$x2-2lnx+a-1-f′(x)=$\frac{1}{2}$x2-2lnx+a-x,
由已知,g(x)≥0,只需$\frac{1}{2}$x2-2lnx+a-x≥0,
即a≥x-$\frac{1}{2}$x2+2lnx,
设h(x)=x-$\frac{1}{2}$x2+2lnx(x>0),
则′(x)=1-x+$\frac{2}{x}$=-$\frac{(x+1)(x-2)}{x}$,
令h′(x)=0,得x=2;令h′(x)>0,得0<x<2;
令h′(x)<0,得x>2,
即有h(x)在(0,2)上是增函数;在(2,+∞)上为减函数.
则h(x)max=h(2)=2ln2,即有a≥2ln2,
故a的范围是[2ln2,+∞).
点评 本题考查导数的运用:求切线方程和单调区间、极值以及最值,同时考查不等式恒成立问题的解法,属于中档题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
12.过点A(0,1)且与双曲线x2-y2=4仅有一个公共点的直线共有( )条.
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
9.设集合A={x|x≤2},则下列四个关系中正确的是( )
| A. | 1∈A | B. | 1∉A | C. | {1}∈A | D. | 1⊆A |
13.若(x-1)7=a0+a1(x+1)+a2(x+1)2+…+a7(x+1)7,则a1等于( )
| A. | -14 | B. | 448 | C. | -1024 | D. | -16 |

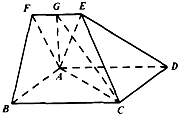 如图,在五面体ABCDEF中,四边形ABCD为正方形,EF∥AD,平面ADEF⊥平面ABCD,且BC=2EF,AE=AF,点G为EF中点.
如图,在五面体ABCDEF中,四边形ABCD为正方形,EF∥AD,平面ADEF⊥平面ABCD,且BC=2EF,AE=AF,点G为EF中点.