题目内容
如图，在棱长为2的正方体ABCD-A1B1C1D1中，E为BC的中点，点P在线段D1E上，点P到直线CC1的距离的最小值为 .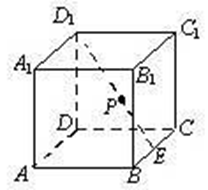
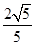
解析
练习册系列答案
教学练新同步练习系列答案
课前课后同步练习系列答案
课堂小作业系列答案
相关题目
教学练新同步练习系列答案课前课后同步练习系列答案课堂小作业系列答案题目内容
如图，在棱长为2的正方体ABCD-A1B1C1D1中，E为BC的中点，点P在线段D1E上，点P到直线CC1的距离的最小值为 .
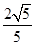
解析
教学练新同步练习系列答案课前课后同步练习系列答案课堂小作业系列答案
A1B1C1D1的棱长为4,M为BD1的中点,N在A1C1上,且|A1N|=3|NC1|,则MN的长为 . 
，E、F分别为AB、CD中点，且EF=4，则AD与BC所成的角是 . 
的棱长为2，则
与平面
间的距离为__________。
的菱形
沿较短对角线
折成二面角
，点
分别为
的中点，给出下列四个命题：
；②
是异面直线
与
；④
.
的二面角
,点A
，
，C为垂足，
，BD
，D为垂足，若AC=BD=DC=1则AB与
面所成角的正弦值为__________
的二面角
,点A
，
，C为垂足，
，BD
，D为垂足，若AC=BD=DC=1则AB与
面所成角的正弦值为__________