题目内容
已知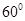 的二面角
的二面角 ,点A
,点A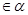 ,
,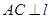 ,C为垂足,
,C为垂足,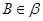 ,BD
,BD ,D为垂足,若AC=BD=DC=1则AB与
,D为垂足,若AC=BD=DC=1则AB与 面所成角的正弦值为__________
面所成角的正弦值为__________
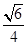
解析试题分析:根据题意,由于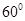 的二面角
的二面角 ,点A
,点A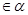 ,
,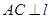 ,C为垂足,
,C为垂足,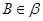 ,BD
,BD ,D为垂足,那么AC=BD=DC=1,则结合向量的数量积的性质可知
,D为垂足,那么AC=BD=DC=1,则结合向量的数量积的性质可知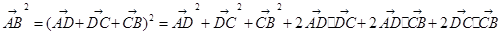
将已知中的长度和角度代入可知结论为1+1+1+2 1
1 1
1
 =2,那么过点A作AE⊥β,交β于点E,连接DE,BE,则∠ABE就是AB与β面所成角.∵AD⊥l,l?β,∴DE⊥l,∴∠ADE=60°,∴AE=AD•sin60°=
=2,那么过点A作AE⊥β,交β于点E,连接DE,BE,则∠ABE就是AB与β面所成角.∵AD⊥l,l?β,∴DE⊥l,∴∠ADE=60°,∴AE=AD•sin60°=
故所求的正弦值为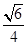 ,故答案为
,故答案为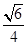 。
。
考点:线面角的求解
点评:本题考查直线与平面所成角的正弦值的求法,具本涉及到向量知识、三垂线定理、二面角等基本知识点,解题时要注意空间思维能力的培养

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
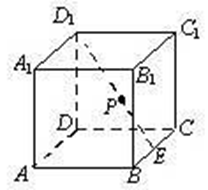
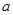 的正方体
的正方体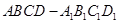 中,
中, 分别是
分别是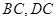 的中点,则异面直线
的中点,则异面直线 与
与 所成角等于
所成角等于 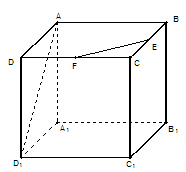
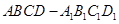 ,底面
,底面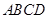 是正方形,
是正方形,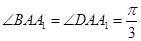 ,则棱
,则棱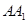 和底面所成角为 。
和底面所成角为 。 ,
, 是两条直线,且
是两条直线,且 不垂直于平面
不垂直于平面 ,那么平面
,那么平面 是异面直线,则直线
是异面直线,则直线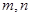 相交,且
相交,且 ∥平面
∥平面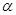 ,则
,则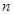 与
与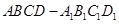 中,二面角
中,二面角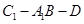 的余弦值为 .
的余弦值为 .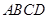 -
- 中,
中,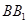 与平面
与平面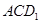 所成角的余弦值为 .
所成角的余弦值为 .  ,其中m∥n,那么在平面
,其中m∥n,那么在平面