题目内容
已知函数f(x)=ax3+bx2-3x(a、b∈R)在点x=-1处取得极大值为2.
(1)求函数f(x)的解析式;
(2)若对于区间[-2,2]上任意两个自变量的值x1、x2,都有|f(x1)-f(x2)|≤c,求实数c的最小值.
(1)求函数f(x)的解析式;
(2)若对于区间[-2,2]上任意两个自变量的值x1、x2,都有|f(x1)-f(x2)|≤c,求实数c的最小值.
(1)f(x)=x3-3x(2)4
(1)f′(x)=3ax2+2bx-3.
由题意,得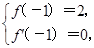 即
即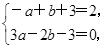 解得
解得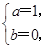
所以f(x)=x3-3x.
(2)令f′(x)=0,即3x2-3=0,得x=±1.
因为f(-1)=2,f(1)=-2,所以当x∈[-2,2]时,f(x)max=2,f(x)min=-2.
则对于区间[-2,2]上任意两个自变量的值x1、x2,都有|f(x1)-f(x2)|≤|f(x)max-f(x)min|=4,所以c≥4.所以c的最小值为4.
由题意,得
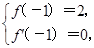 即
即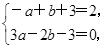 解得
解得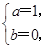
所以f(x)=x3-3x.
(2)令f′(x)=0,即3x2-3=0,得x=±1.
| x | -2 | (-2,-1) | -1 | (-1,1) | 1 | (1,2) | 2 |
| f′(x) | | + | | - | | + | |
| f(x) | -2 | 增 | 极大值 | 减 | 极小值 | 增 | 2 |
则对于区间[-2,2]上任意两个自变量的值x1、x2,都有|f(x1)-f(x2)|≤|f(x)max-f(x)min|=4,所以c≥4.所以c的最小值为4.

练习册系列答案
相关题目
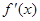 是
是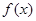 的导函数,
的导函数,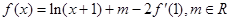 ,且函数
,且函数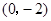 .
.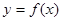 的表达式;
的表达式;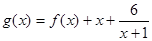 的单调区间和极值.
的单调区间和极值.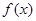
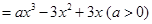
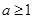 时,求
时,求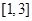 的最大值为
的最大值为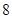 ,求
,求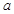 的值.
的值.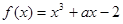 在区间
在区间 内是增函数,则实数
内是增函数,则实数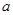 的取值范围是
的取值范围是 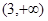
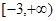
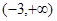
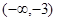
 ,求f(x)在[-1,1]上的最小值;
,求f(x)在[-1,1]上的最小值;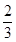 x+
x+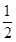 ,h(x)=
,h(x)=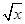 ,设F(x)=f(x)-h(x),求F(x)的单调区间与极值.
,设F(x)=f(x)-h(x),求F(x)的单调区间与极值. ,g(x)=x2-2ax+4,若任意x1∈[0,1],存在x2∈[1,2],使f(x1)≥g(x2),则实数a的取值范围是______.
,g(x)=x2-2ax+4,若任意x1∈[0,1],存在x2∈[1,2],使f(x1)≥g(x2),则实数a的取值范围是______.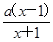 ,若函数f(x)在(0,+∞)上为增函数,则a的取值范围是________.
,若函数f(x)在(0,+∞)上为增函数,则a的取值范围是________.