题目内容
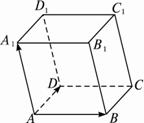
 如图已知平行六面体ABCD-A′B′C′D′,E、F、G、H分别是棱A′D′、D′C′、C′C和AB的中点,求证E、F、G、H四点共面.
如图已知平行六面体ABCD-A′B′C′D′,E、F、G、H分别是棱A′D′、D′C′、C′C和AB的中点,求证E、F、G、H四点共面.分析:取
=
,
=
,
=
,则根据平行六面体的性质和向量加法法则得
=
+
+
=
+2
+
.结合空间向量的线性运算法则,化简得
=
-
,可得向量
与
、
是共面向量.由此即可证出E、F、G、H四点共面.
| ED′ |
| a |
| EF |
| b |
| EH |
| c |
| HG |
| HB |
| BC |
| CG |
| D′F |
| ED′ |
| 1 |
| 2 |
| AA′ |
| HG |
| 3 |
| 2 |
| b |
| 1 |
| 2 |
| c |
| HG |
| EF |
| EH |
解答:解:取
=
,
=
,
=
,则
∵多面体ABCD-A′B′C′D′是平行六面体,
且E、F、G、H分别是棱A′D′、D′C′、C′C和AB的中点,
∴
=
=
-
,
=2
=2
,且
=
,
=
+
+
=
+2
+
=(
-
)+2
+
(
+
+
)=
+
+
(
-
-
-
)=
-
,
∴
与
、
共面,即
与
、
共面
由此可得E、F、G、H四点共面.
| ED′ |
| a |
| EF |
| b |
| EH |
| c |

∵多面体ABCD-A′B′C′D′是平行六面体,
且E、F、G、H分别是棱A′D′、D′C′、C′C和AB的中点,
∴
| HB |
| D′F |
| b |
| a |
| BC |
| ED′ |
| a |
| CG |
| 1 |
| 2 |
| AA′ |
| HG |
| HB |
| BC |
| CG |
| D′F |
| ED′ |
| 1 |
| 2 |
| AA′ |
=(
| b |
| a |
| a |
| 1 |
| 2 |
| AH |
| HE |
| EA′ |
| b |
| a |
| 1 |
| 2 |
| b |
| a |
| c |
| a |
| 3 |
| 2 |
| b |
| 1 |
| 2 |
| c |
∴
| HG |
| b |
| c |
| HG |
| EF |
| EH |
由此可得E、F、G、H四点共面.
点评:本题给出平行六面体的棱的中点,求证E、F、G、H四点共面.着重考查了空间向量的加法法则、线性运算法则和平行六面体的性质等知识,属于中档题.

练习册系列答案
相关题目
 已知平行六面体ABCD-A′B′C′D′中,AB=4,AD=3,AA′=5,∠BAD=90°,∠BAA′=∠DAA′=60°,
已知平行六面体ABCD-A′B′C′D′中,AB=4,AD=3,AA′=5,∠BAD=90°,∠BAA′=∠DAA′=60°, 如图,已知平行六面体OABC-O1A1B1C1,点G是上底面O1A1B1C1的中心,且
如图,已知平行六面体OABC-O1A1B1C1,点G是上底面O1A1B1C1的中心,且 如图,已知平行六面体ABCD-A1B1C1D1.
如图,已知平行六面体ABCD-A1B1C1D1.